SOCI208 - Module 15 - Simple Linear Regression

1.  Functional & Statistical Relations

A functional relation between a dependent variable Y and an independent variable X is an exact relation: the value of Y is uniquely determined when the value of X is specified.


A statistical relation between a dependent variable Y and an independent variable X is an inexact relation; the value of Y is not uniquely determined when the value of X is specified.

NOTE:  the solid line in previous exhibit is estimated by the LOWESS algorithm, which is one form of nonparametric regression which we will look at later

"line or curve of statistical relationship" = tendency of Y to vary systematically as a function of X

2.  Simple Linear Regression Model

1.  Development of the Model

In the most general form, the regression model formalizes the two ingredients of a statistical relation: The regression model thus has two components The two components are represented as in the following exhibit.
  • Exhibit:  Pictorial representation of simple linear regression model (NWW figure 18.4 p. 535) [m15006.gif]
  • Exhibit:  Pictorial representation of simple linear regression model  (NKNW F1.6 p. 12)

    • 2.  Simple Linear Regression Model

    When the regression function is linear, the simple linear regression model is written
    Yi = b0 + b1Xi + ei   i = 1, 2, ..., n
    where
    Yi is the value of the dependent variable for the ith observation
    Xi is the value of the independent (predictor) variable for the ith element, and is assumed to be a known constant
    b0 and b1 are parameters (or coefficients)
    ei are independent ~N(0,s2)

    3.  Component 1 - Error Term

    The assumption that the ei are independent ~N(0,s2) implies that
    1. the ei are normally distributed RVs
    2. E{ei} = 0 (the expected value of each error term ei is 0)
    3. s2{ei} = s2 (the variance of each ei is the same at all levels of X, and equal to s2, which denotes a constant number)
    4. ei and ej are uncorrelated RVs so that their covariance is zero (i.e., s{ei, ej} = 0 for all i,j such that i <> j)
    Q - Is it reasonable to assume that error terms are normally distributed?
    A - To the extent that the error term ei represents the sum of the effects of factors that are not explicitly included as independent variables in the model, and that these effects are additive and relatively independent, ei will tend to behave as predicted by the CLT, i.e. be normally distributed when the number of factors is large.

    4.  Component 2 - Regression Function

    The regression function represents the systematic part of the model, corresponding to the line or curve of statistical relationship.
    The regression function aka response function relates E{Y}, the expected value or mean of Y, to the value of the independent variable X.  In the simple linear regression model the regression function is
    E{Y} = b0 +  b1X
    Derivation of Regression Function
    From the simple linear regression model
    E{Yi} = E{b0 +  b1Xi + ei} = b0 +  b1Xi + E{ei}
    Since E{ei} = 0 it follows that
    E{Yi} = b0 +  b1Xi
    or, in general for any value of X
    E{Y} = b0 +  b1X

    The graph of the regression function is called the regression line.
    The parameters b0 and b1X are called regression coefficients or regression parameters.
    The meaning of each coefficient is as follows

    This is illustrated in the next exhibit.
  • Exhibit: Regression of % clerks on seasonality showing the meanings of b0 and b1 [m15008.gif]
    • Q - What is the meaning of the slope (-.169) in the regression of % clerks on the seasonality index?
    Q - What is the meaning of the intercept (14.631)?  Is the intercept substantively meaningful here?
     

    5.  Component 3 - Probability Distribution of Y

    The variance of Yi is
    s2{Yi} =  s2{b0 +  b1Xi + ei} =  s2{ei} =  s2
    since ei is the only RV in the expression, and the variance of the eror ei is assumed the same (= s2 ) regardless of the value of X.

    3.  Point Estimation of b0 and b1

    1. Least Squares

    The regression coefficients b0 and b1 are usually unknown.  They can be estimated from a sample with n observations on Y and X with the method of least squares.  The method of least squares (or OLS for "Ordinary Least Squares") consists in finding estimates b0 and b1 of b0 and b1 which minimize the quantity Q, which is the sum of the squared deviations Yi - ( b0 + b1Xi) of Yi from its expected value.
    Q = Si=1 to n (Yi - b0 - b1Xi)2
    The following exhibit shows the Y (vertical) deviations ei that are squared and summed up to evaluate Q (although in this case the regression line is already the OLS solution) Q can be minimized by: One can calculate SYi, SXi, SXiYi, and SXi2 from sample observations, and then solve the normal equations for b0 and b1.
    Or, equivalently, one can use the formula
    b1 = (S(Xi - X.)(Yi - Y.))/S(Xi - X.)2
    b0 =  Y. - b1X.
    (calculating b1 first, then b0)
    Q - What is the meaning of these formulas?
    (Optional) Derivation of b0 and b1 Using Calculus
    To find the values of b0 and b1 that minimize
    Q = Si=1 to n (Yi - b0 - b1Xi)2  
    one differentiates Q with respect to  b0 and b1, obtaining
    dQ/db0 = -2Si=1 to n (Yi - b0 - b1Xi)
    dQ/db1 = -2Si=1 to n Xi(Yi - b0 - b1Xi)   
    The particular values, denoted b0 and b1, that minimize Q are found by setting these derivatives to zero, as
    -2Si=1 to n (Yi - b0 - b1Xi) = 0
    -2Si=1 to n Xi(Yi - b0 - b1Xi) = 0
    and solving for b0 and b1.
    Solving is done by simplifying and expanding these equations and rearranging the terms to produce the normal equations
    SYi = nb0 + b1SXi
    SXiYi = b0SXi + b1SXi2      
    presented earlier.

    Table 1 shows how the regression coefficients can be calculated using these formulas for the Stinchcombe data (elements are sectors of the construction industry, Yi is % clerks, and Xi is an index of seasonality of employment).
     
    Table 1 .  Calculations for OLS Estimates b0 and b1
    i
    		 Sector Xi Yi (Xi - X.) (Yi - Y.) (Xi - X.)2 (Yi - Y.)2 (Xi - X.)
    x (Yi - Y.)
    1 STRSEW 73 4.8 33.444 -3.156 1118.531 9.958 -105.536
    2 SAND 43 7.6 3.444 -0.356 11.864 0.126 -1.225
    3 VENT 29 11.7 -10.556 3.744 111.420 14.021 -39.525
    4 BRICK 47 3.3 7.444 -4.656 55.420 21.674 -34.658
    5 GENCON 43 5.2 3.444 -2.756 11.864 7.593 -9.491
    6 SHEET 29 11.7 -10.556 3.744 111.420 14.021 -39.525
    7 PLUMB 20 10.9 -19.556 2.944 382.420 8.670 -57.580
    8 ELEC 13 12.5 -26.556 4.544 705.198 20.652 -120.680
    9 PAINT 59 3.9 19.444 -4.056 378.086 16.448 -78.858
    Total 356 71.6 -0.000 0.000 2886.222 113.162 -487.078
    Mean 39.556 7.956

    b0 and b1 are then calculated using the formulas above as

    b1 = (-487.078)/(2886.222) = -0.169
    b0 = (7.956) - (-0.169)(39.556) = 14.631
    (The slope b1 can also be calculated as the ratio of the same two numbers, each divided by n-1, i.e. as the sample covariance of X and Y, denoted sXY, divided by the variance of X, denoted sX2, as
    b1 = sXY/sX2
    b0 =  Y. - b1X.                                               )

    2. Properties of LS estimators

    Under the assumptions of the regression model (minus the assumption of normality of ei, which is not necessary for these results), the Gauss-Markov theorem states that b0 and b1 are the BLUE, i.e. the We will prove the Gauss-Markov theorem later in SOCI209 in the multiple regression context.
    Note that the Gauss-Markov theorem holds even though the shape of the distribution of the errors is not specified (e.g., it needs not be normal).

    4.  Point Estimation of Mean Response E{Yh}

    1.  Estimated Regression Function

    The regression function E{Y} = b0 + b1X is estimated as
    ^Y = b0 + b1X
    where ^Y ("Y hat") is the estimated regression function at level X of the independent variable.
    (^Y is also called predictor or estimate of Y; ^Yi is called the fitted value of Y for observation i.)
    An extension of Gauss-Markov theorem states that ^Y is also the BLUE of E{Y}.
    Example: in the Stinchcombe study,
    ^Y = 14.631 - (0.169)X is the estimated regression function
    ^Y8 = 14.631 - (0.169)(13) = 12.437 is the fitted value for observation 8 (ELEC)

    2.  Mean Response E{Yh}

    The mean response E{Yh} is the expected value of Y when X = Xh, i.e.
    E{Yh} = b0 + b1Xh
    where Xh denotes a specified level of X that does not necessarily correspond to the value Xi of an observation in the sample.

    3.  Point Estimator of E{Yh}

    The point estimator of the mean response E{Yh} is the value of the estimated regression function for X = Xh, i.e.
    ^Yh = b0 + b1Xh
    Example: if a sector of the construction industry had a seasonality score Xh =  35 (a value not found in the data set), the estimated mean response would be
    ^Yh = 14.631 - (0.169)(35) = 8.716

    5.  Residuals

    1.  Calculation of the Residual ei

    The ith residual ei is the difference between Yi and ^Yi, i.e.
    ei = Yi - ^Yi
    so ei corresponds to the vertical discrepancy between Yi and the corresponding point ^Yi on the regression line.

    2.  Distinction Between ei and ei

    ei is not the same as ei, i.e.

    3.  Properties of OLS Residuals

    Properties of fitted values and residuals: (See derivations in NWW p. 548.)

    6.  Analysis of Variance (ANOVA)

    This is easy and illuminating.
    (Note for later: ANOVA results generalize immediately to multiple regression; the only difference is that ^Yi will be calculated using several independent variables instead of one independent variable, and the degrees of freedom (see later) will be adjusted accordingly.)

    1.  Partitioning of Sum of Squares Total

    The principle of ANOVA is shown in the next figure.  (Understanding this figure is very important for understanding ANOVA.) From the figure, one can see that the total variation in Yi, (Yi - Y.), can be decomposed into two components:
     
    Decomposition ot Total Variation in Yi
    Yi - Y.
    =
    ^Yi - Y.
    +
    Yi - ^Yi
    total deviation of Yi from mean
    deviation of fitted value from mean
    deviation of Yi from fitted value

    One defines sums of squares corresponding to each deviation:
     

    Sums of Squares
    Symbol
    SSTO
    SSR
    SSE
    Formula
    S(Yi - Y.)2
    S(^Yi - Y.)2
    S(Yi - ^Yi)2
    Name
    sum of squares total
    sum of squares regression
    sum of squares error or "residual" sum of squares
    Meaning
    total variation in Y
    variation in Y "accounted for" by regression line
    variation in Y around regression line

    The basic ANOVA result is:
     

    SSTO
    =
    SSR
    +
    SSE
    OR:
    S(Yi - Y.)2
    =
    S(^Yi - Y.)2
    +
    S(Yi - ^Yi)2

    This is actually a remarkable and non-obvious property that must be proven!  (See optional proof in NWW p. 552 (bottom).)
    Table 2 shows the calculations of ANOVA sums of squares for the regression of % clerks (Y) on employment seasonality (X).
     
    Table 2.  Calculations for ANOVA Sums of Squares
    i
    Sector
    Xi
    Yi
    ^Yi
    ei
    		 (Yi - Y.)2 (^Yi - Y.)2 (Yi - ^Yi)2
    1 STRSEW 73 4.8 2.311 2.489 9.958 31.856 6.193
    2 SAND 43 7.6 7.374 0.226 0.126 0.338 0.051
    3 VENT 29 11.7 9.737 1.963 14.021 3.173 3.854
    4 BRICK 47 3.3 6.699 -3.399 21.674 1.578 11.555
    5 GENCON 43 5.2 7.374 -2.174 7.593 0.338 4.727
    6 SHEET 29 11.7 9.737 1.963 14.021 3.173 3.854
    7 PLUMB 20 10.9 11.256 -0.356 8.670 10.891 0.127
    8 ELEC 13 12.5 12.437 0.063 20.652 20.084 0.004
    9 PAINT 59 3.9 4.674 -0.774 16.448 10.768 0.599
    Total 356 71.6 113.162 82.199 30.963
    Mean 39.556 7.956
    = SSTO
    = SSR
    = SSE
    b1 = -0.169
    b0 = 14.631

    Alternative computational formulas are:

    2.  Partitioning of Degrees of Freedom

    To each sum of squares correspond degrees of freedom (df).  Degrees of freedom are additive.
     
     
    Degrees of Freedom of ANOVA Sums of Squares
    n - 1
    =
    1
    +
    (n - 2)
    df for SSTO
    df for SSR
    df for SSE
    1 df lost estimating Y.
    (cf. sample variance s2)
    1 df lost estimating b1
    2 df lost estimating
    b0 and b1

    3. Mean Squares

     Mean squares are the sums of squares divided by their respective df.  Mean squares are not additive.
     
    Mean Squares
    s2(Y)
    MSR
    MSE
    SSTO/(n - 1)
    SSR/1
    SSE/(n - 2)
    sample variance of Y
    regression mean square
    error mean square

    MSE is an estimator of s2, the variance of e.
    (This makes sense since MSE is the sum of the squared residuals divided by the df of this sum, which is n-2.)
    It can be shown that MSE is an unbiased estimator of s2, i.e.

    E{MSE} = s2
    (MSE)1/2, called the standard error of estimate, is an estimator of s, the standard deviation of e.

    4. ANOVA Table

    The ANOVA table summarizes all this information. Table 3 shows the ANOVA table for the regression of % clerks on employment seasonality.
     
    Table 3.  ANOVA Table for Stinchcombe Data
    Source Sum of Squares df Mean Squares F-ratio
    Regression 82.199   1 82.199 18.583
    Error 30.963 7 4.423
    Total 113.162 8 14.145

    The F-ratio is calculated as the ratio F* = MSR/MSE (here 82.199/4.423 = 18.583); the meaning of F* is discussed in Module 16.

    Q - What are the meanings of the quantities 4.423 and 14.145 in Table 3?

    7.  Coefficients of Determination & Correlation

    1.  Coefficient of Determination or "R-square"

    The following formulas are equivalent:
    r2 = (SSTO - SSE)/SSTO = SSR/SSTO = 1 - SSE/SSTO
    where 0 <= r2 <= 1

    Example: In the regression of % clerks on seasonality the r2 can be calculated equivalently as

    (113.162 - 30.963)/113.162 = 82.199/113.162 = 1 - (30.963/113.162) = 0.726
    Limiting cases: From the formulas one sees that r2 can be interpreted as the proportion of the variation in Y "explained" by the regression model.
    (But note that "variation" refers to the sum of squared deviations, so variation is not measured in linear units.  So interpretation of r2 is not as intuitive as it may seem.)

    2.  Coefficient of Correlation

    The following formulas are equivalent:
    r = +/- (r2)1/2 = (S(Xi - X.)(Yi - Y.))/(S(Xi - X.)2S(Yi - Y.)2)1/2
    The "+/-" means that r takes the sign of b1.
    The second formula is equivalent to the ratio of the covariance of X and Y divided by the square root of the product of the variances of X and of Y.  (Since each variance and covariance is divided by (n - 1) the divisor cancels out.)
    When r2 is not 0 or 1,
    |r| > r2
    so that the psychological impact (or propaganda value) of r is stronger than that of r2.
    Example: In the regression of % clerks on seasonality the r2 is 0.726 and the correlation coefficient r is -.852.
    Examples of the degree of association corresponding to various values of r are shown in the next exhibit. The correlation coefficient r alone can give a misleading idea of the nature of a statistical relationship, so it is important to always look at the scatterplot of the relationship.

    3.  Standardized Regression Coefficient (Mostly Useful in Multiple Regression Context)

    The standardized regression coefficient  b1* is  calculated as:
    b1*  =  b1(sX/sY)
    which in the simple linear regression model is equal to r.  (This is no longer true in the multiple regression model.)
    Conversely, recover the (unstandardized) regression coefficient from the standardized one as
    b1  =   b1*(sY/sX)   ( = r(sY/sX), in simple linear regression only)
    where sX and sY are the sample standard deviations of X and Y, respectively.
    b1* indicates the change in the mean response E{Y}, measured in units of standard deviation of Y, associated with an increase in X of one standard deviation of X.
    Standardized coefficients are more useful in the multiple regression model, where they permit comparing the relative magnitudes of the coefficients of independent variables measured in different units (such as a variable measured in years, and another measured in thousands of dollars).

    8.  Simple Linear Regression in Practice

    1.  SYSTAT Examples

    >USE "Z:\mydocs\ys209\sexdipri.syd"
    SYSTAT Rectangular file Z:\mydocs\ys209\sexdipri.syd,
    created Tue Apr 23, 2002 at 08:35:28, contains variables:
     SPECIES$     LENGTHDI     WEIGHTDI     MEANHARE     MAXHARE

    >rem relationship berween sex dimorphism (length ration male to female) and
    >rem mean harem size in primates, a measure of sexual competition among males
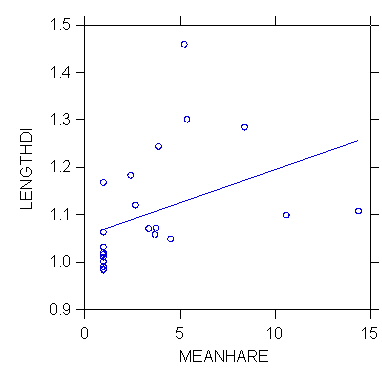
    >regress
    >model lengthdi=constant+meanhare
    >estimate

    Dep Var: LENGTHDI   N: 22   Multiple R: 0.403   Squared multiple R: 0.162

    Adjusted squared multiple R: 0.120   Standard error of estimate: 0.115

    Effect         Coefficient    Std Error     Std Coef Tolerance     t   P(2 Tail)
    CONSTANT             1.055        0.035        0.000      .      29.949    0.000
    MEANHARE             0.014        0.007        0.403     1.000    1.967    0.063

    Analysis of Variance
    Source             Sum-of-Squares   df  Mean-Square     F-ratio       P

    Regression                 0.051     1        0.051       3.870       0.063
    Residual                   0.266    20        0.013

    -------------------------------------------------------------------------------
    *** WARNING ***
    Case           17 has large leverage   (Leverage =        0.487)
    Case           19 is an outlier        (Studentized Residual =        3.821)

    Durbin-Watson D Statistic          1.949
    First Order Autocorrelation       -0.026

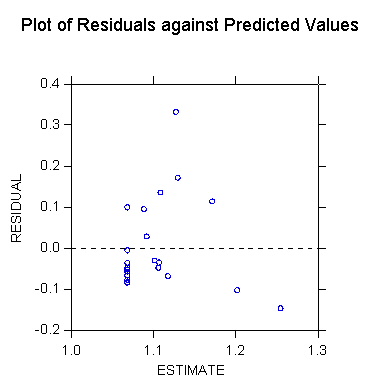
    >plot lengthdi*meanhare/stick=out smooth=linear short


     
     

    >USE "Z:\mydocs\ys209\yule.syd"
    SYSTAT Rectangular file Z:\mydocs\ys209\yule.syd,
    created Wed Feb 17, 1999 at 09:34:32, contains variables:
     UNION$       PAUP         OUTRATIO     PROPOLD      POP

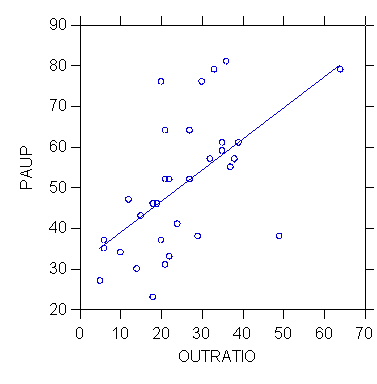
    >model paup=constant+outratio
    >estimate

    Dep Var: PAUP   N: 32   Multiple R: 0.594   Squared multiple R: 0.353
    Adjusted squared multiple R: 0.331   Standard error of estimate: 13.483

    Effect         Coefficient    Std Error     Std Coef Tolerance     t   P(2 Tail)
    CONSTANT            31.089        5.324        0.000      .       5.840    0.000
    OUTRATIO             0.765        0.189        0.594     1.000    4.045    0.000

    Analysis of Variance
    Source             Sum-of-Squares   df  Mean-Square     F-ratio       P
    Regression              2973.751     1     2973.751      16.359       0.000
    Residual                5453.468    30      181.782

    -------------------------------------------------------------------------------
    *** WARNING ***
    Case           15 has large leverage   (Leverage =        0.328)

    Durbin-Watson D Statistic          1.853
    First Order Autocorrelation       -0.018


     

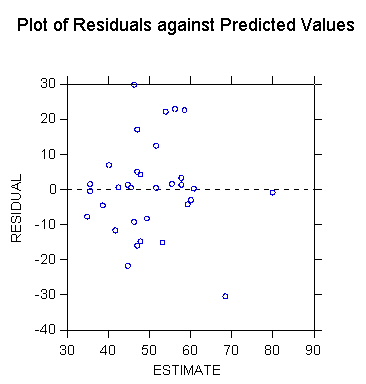
    >plot paup*outratio/stick=out smooth=linear short


     
     

    2. STATA Examples

    . set mem 32000
    (32000k)

    . use "Z:\mydocs\S208\gss98.dta", clear

    . su income

        Variable |     Obs        Mean   Std. Dev.       Min        Max
    -------------+-----------------------------------------------------
          income |    2699    10.85624   2.429604          1         13

    . su  educ

        Variable |     Obs        Mean   Std. Dev.       Min        Max
    -------------+-----------------------------------------------------
            educ |    2820    13.25071   2.927512          0         20

    . regress income educ

          Source |       SS       df       MS              Number of obs =    2688
    -------------+------------------------------           F(  1,  2686) =  235.66
           Model |  1269.91329     1  1269.91329           Prob > F      =  0.0000
        Residual |  14474.0495  2686  5.38870049           R-squared     =  0.0807
    -------------+------------------------------           Adj R-squared =  0.0803
           Total |  15743.9628  2687  5.85930882           Root MSE      =  2.3214

    ------------------------------------------------------------------------------
          income |      Coef.   Std. Err.      t    P>|t|     [95% Conf. Interval]
    -------------+----------------------------------------------------------------
            educ |   .2359977   .0153731    15.35   0.000     .2058533    .2661421
           _cons |    7.71967   .2094621    36.85   0.000     7.308947    8.130393
    ------------------------------------------------------------------------------
     

    9.  Historical Note

    The method of least squares (French "moindres carrés") was developed by Adrien Legendre in the context of reconciling astronomical observations; it was first published in 1805.  Try your French on Legendre's appendix below (but be aware today's notation is different from Legendre's).



    Last modified 10 Jan 2003