SOCI709 (formerly 209) - Module 1 - SIMPLE LINEAR REGRESSION

1.  Introduction

Regression analysis is "a statistical methodology that utilizes the relation between two or more quantitative variables so that one variable [the dependent or response variable] can be predicted from the other, or others [the independent or predictor variables]."  (ALSM5e p. 3)
Examples:

 2.  Functional & Statistical Relations

A functional relation between a dependent variable y and an independent variable X is an exact relation: the value of y is uniquely determined when the value of X is specified.
Examples: A statistical relation between a dependent variable y and an independent variable x is an inexact relation; the value of y is not uniquely determined when the value of X is specified. (NOTE:  the solid line in previous exhibit is estimated by the LOWESS algorithm, which is one form of nonparametric regression which we will look at later.)

The line or curve of statistical relationship refers to the tendency of y to vary systematically as a function of x.

3.  Simple Linear Regression Model

1.  Population Model

The idea of a statistical relationship can be formalized as in the following two exhibits.  The first exhibit depicts the more general situation in which the regression function, or line tracing the means of Y as function of X, is not necessarily linear (it is said to be curvilinear).
  • Exhibit:  Pictorial representation of general regression model  (ALSM5e F1.4 p. 7) [m1004.gif]
    • The second exhibit shows a situation where the regression function is linear.
  • Exhibit:  Pictorial representation of simple linear regression model  (ALSM5e F1.6 p. 12) [m1005.gif]
    • The regression model is the formalization of the idea of a statistical relation; it translates the idea into two components: When the regression function is linear, the simple linear regression model is written
    Yi = b0 + b1Xi + ei   i = 1, 2, ..., n            (1)
    where Greek letters b0, b1 and e are used for the regression coefficients and the error term to indicate that the regression model pertainins to the population from which the sample is drawn; these parameters are not directly known and must be estimated from sample data.
    The two components of a statistical relation are translated in the simple regression model as Model (1) is called

    2.  Assumptions on the Error Term

    There are two nested sets of assumptions concerning the distribution of the error term; the second set adds the assumption of normality of the errors.
    1.  Distribution of Errors Unspecified
    ei is a random error term
    2.  Distribution of Errors Normal
    To the first set add the assumption that distribution of ei is normal.  Then the entire set of assumptions (including the normality one) can be expressed simply as Q - Is it reasonable to assume that error terms are normally distributed?
    A - To the extent that the error term ei represents the sum of the effects of factors that are not explicitly included as independent variables in the model, and that these effects are additive and relatively independent, ei will tend to behave as predicted by the Central Limit Theorem (CLT), i.e. be normally distributed when the number of factors is large.

    Assumption of normality of the errors is necessary to theoretically justify statistical inference (see Module 2), especially in small samples.  But most properties of least squares estimators of model parameters do not depend on the normality assumption.

    3.  Components of Simple Regression Model

    The regression function or response function  represents the systematic part of the model; it relates the expected value (or mean) E{Y} of Y to the value of the independent variable X.  The graph of the regression function is called the regression line.  In the simple linear regression model the regression function for any value of X is
    E{Y} = E{b0 +  b1Xi + ei} =  b0 +  b1Xi + E{ei} = b0 +  b1X
    since by assumption E{ei} = 0.

    The parameters b0 and b1 are called regression coefficients or regression parameters.
    The meaning of each coefficient is as follows

    With respect to the regression model the population variance of Yi is
    s2{Yi} = s2{b0 +  b1Xi + ei} =  s2{ei} =  s2
    where s2 is the variance of ei.  This is because ei is the only random variable in the expression, and the variance of the error ei is assumed to be the same and equal to s2 regardless of the value of X.  (This definition of the population variance of Y as s2 , i.e., the variance of ei, may be confusing as it does not corresponds directly to the sample variance of Y, Sy2 .  It is helpful to consider that s2{Yi} actually means "variance of y around the regression line", so an equivalent expression for s2{Yi} is s2{Y|X}, or "variance of Y (around the regression line) given a certain value of X".)

    The quantities b0 and b1 and  s2 are the parameters of the regression model; they have to be estimated from the data.  (In reality one estimates  b0 and b1 and then the estimate of s2 is obtained as a by-product.)

    4.  An Example of Simple Linear Regression

    Table 1 shows data on 9 sectors of the construction industry in Ohio in 19?? (Stinchcombe 19??).  The dependent variable y is the percentage of clerks (white-collar workers) in the labor force of a sector, a measure of bureaucratization.  The independent variable X is a measure of seasonality (seasonal variation in sector activity).  Data for the nine sectors are shown in Table 1.  The index i (i=1,...,9) refers to each sector.  The author of the study theorized that more seasonal sectors should  be less bureaucratic , i.e., have lower percentages of clerks in their labor forces.
     
     
    Table 1 .  Calculations for OLS Estimates b0 and b1
    i
    		 Sector Xi Yi (Xi - X.) (Yi - Y.) (Xi - X.)2 (Yi - Y.)2 (Xi - X.)
    x (Yi - Y.)
    1 STRSEW 73 4.8 33.444 -3.156 1118.531 9.958 -105.536
    2 SAND 43 7.6 3.444 -0.356 11.864 0.126 -1.225
    3 VENT 29 11.7 -10.556 3.744 111.420 14.021 -39.525
    4 BRICK 47 3.3 7.444 -4.656 55.420 21.674 -34.658
    5 GENCON 43 5.2 3.444 -2.756 11.864 7.593 -9.491
    6 SHEET 29 11.7 -10.556 3.744 111.420 14.021 -39.525
    7 PLUMB 20 10.9 -19.556 2.944 382.420 8.670 -57.580
    8 ELEC 13 12.5 -26.556 4.544 705.198 20.652 -120.680
    9 PAINT 59 3.9 19.444 -4.056 378.086 16.448 -78.858
    Total 356 71.6 -0.000 0.000 2886.222 113.162 -487.078
    Mean 39.556 7.956

    The next exhibit shows a scatterplot in which each point corresponds to the pair of values (yi, xi), with y measured on the vertical axis and x measured on the horizontal axis.

  • Exhibit: Graph of simple linear regression of % clerks (Y) on seasonality (X) [m15001.jpg]
    • The solid line is the estimated regression line.  It is represented by the equation
    ^y = b0 + b1x
    where ^y (called "y hat") represents the vertical coordinate of a point on the regression line corresponding to horizontal coordinate x.  The coefficient b0 and b1 are calculated by the method of least squares (explained below).  The model implies that for each observation in the sample the vertical coordinate yi of a point is given by the formula
    yi = ^yi + ei    or
    yi = b0 + b1xi + ei    (i = 1, ..., 9)
    where ei corresponds to the vertical deviation between the observed value yi and ^yi (called the fitted value or predictor of y) implied by the regression line.  ei is called the residual for observation i. b0 and b1 are the (estimated) regression coefficients.  Their meaning is the same as that of the population parameters, i.e. For the construction industry data the slope b1= -.169 in the regression of Y (%clerks) on X (seasonality index) means that for each increase of one unit of seasonality, % clerks decreases by .169 of a percent.  The intercept b0 = 14.631 means that in a sector with no seasonality (x=0), % clerks would be 14.6 percent.  (Q - Is this value of the intercept substantively meaningful here?)

    Note that the simple regression model establishes an asymmetry between the dependent variable y and independent variable x, because deviations are measured along the dependent  variable dimension (usually the vertical axis).  In general a different regression line is obtained if one exchange y and x in their roles.  The choice of one variable as dependent and the other as independent is a substantive choice.  (Correlational models do not assume this asymmetry.)

    4.  Least Squares (OLS)

    1.  Estimation of b0 and b1

    The coefficients of the regression line (regression coefficients) are originally unknown.  They can be estimated from a sample containing n observations on y and x with the method of least squares.  The method of least squares (or OLS for ordinary least squares) consists in finding values for b0 and b1 that minimize the sum (over all observations) of the squared vertical deviations ei of the observed value Yi from the predicted value ^yi on the regression line.  Mathematically, one wants to find the values of b0 and b1 that minimize the quantity Q defined as
    Q = Si=1 to n (yi - b0 - b1xi)2
    The following exhibit shows the vertical deviations ei that are squared and summed up to evaluate Q. To minimize Q one could: (1) use a "brute force" numerical search using a grid of values for b0 and b1 (this is actually what computers can do in situations), or (2) take advantage of the analytical solution originally discovered by French mathematician Legendre.  Legendre discovered that the values b0 and b1 that minimize Q are given by the formulas
    b1 = (S(Xi - X.)(Yi - Y.))/S(Xi - X.)2
    b0 =  Y. - b1X.
    called the normal equations.  All the sums are over all observations (from i=1 to n).  Table 1 shows how one can organize the calculations for the construction industry data.  In the table units are sectors of the construction industry, yi stands for % clerks, and xi for the index of employment seasonality.  One calculates b1first, then b0.  Thus having calculated the sums of squares and cross-products one calculates b0 and b1 using the formulas above as
    b1 = (-487.078)/(2886.222) = -0.169
    b0 = (7.956) - (-0.169)(39.556) = 14.631
    Note that the slope b1 could also be calculated as the ratio of the same two numbers, each divided by n-1, i.e. as the sample covariance of x and y, denoted sxy, divided by the variance of x, denoted sx2, as
    b1 = sXY/sX2
    b0 =  Y. - b1X.
    In practice one uses a computer program to carry out the calculations.  The next exhibit shows a typical simple regression output.

    2.  Estimation of Other Aspects of the Model

    Aspects of the population model that may be of substantive interest are shown in Table 2.
      
    Table 2.  Aspects of Population Regression Model and Point Estimators
    Aspect of the Population Model Symbolic Form Estimate
    Regression coefficients b0 , b1  b0, b1
    Mean response (regression function for given value Xh of X, whether or not Xh is represented in the sample) E{Yh} = b0+ b1Xh ^Yh = b0 + b1Xh
    Estimate, predictor or fitted value of Y (for Xi in the sample) E{Yi} = b0+ b1Xi ^Yi = b0 + b1Xi
    Predicted value of Y for known value Xh of X (Xh not necessarily in the sample) Yh = b0+ b1Xh + e  ^Yh = b0 + b1Xh
    Residual (Xi in the sample) ei ei = Yi - ^Yi
    Residual variance (variance of ei) s2  MSE = SSE/(n-2)
    Standard error of estimate (standard deviation of ei) s MSE1/2
    MSE and SSE are explained later.
    Examples from the construction industry study: It is important to always distinguish between parameter and estimate.  For example ei is not the same as ei, i.e.

    5.  (Optional) Derivation of Least Squares Formulas and Properties of LS Residuals

    1.  Derivation of Formulas for b0 and b1 (Uses Calculus)

    The sum of squared deviations
    Q = Si=1 to n (Yi - b0 - b1Xi)2
    can be viewed as a function of two variables, b0 and b1.  To find the values of  b0 and b1 that minimize Q one differentiates the function in turn with respect to b0 and with respect to b1, obtaining
    dQ/db0 = -2Si=1 to n (Yi - b0 - b1Xi)
    dQ/db1 = -2Si=1 to n Xi(Yi - b0 - b1Xi)
    The values b0 and b1 that minimize Q are found by setting the derivatives to zero, as
    -2Si=1 to n (Yi - b0 - b1Xi) = 0
    -2Si=1 to n Xi(Yi - b0 - b1Xi) = 0
    and solving for b0 and b1.  Solving is done by simplifying and expanding these equations and rearranging the terms to produce the normal equations
    SYi = nb0 + b1SXi
    SXiYi = b0SXi + b1SXi2
    One can also derive the normal equations (although not demonstrate that their solution provides the values of b0 and b1 that minimize the sum of squared residuals) by multiplying through the equation Y=b0+b1X in turn by 1 and by X, and summing the products over all observations.  This observation presages the multiple regression model seen later.

     2.  Properties of OLS Residuals

    Properties of fitted values ^Yi and residuals ei: (See derivations in ALSM5e pp. <> )

    6.  Analysis of Variance (ANOVA)

    Analysis of variance (ANOVA) in the regression context is easy and illuminating.  One should note that ANOVA results for simple linear regression generalize immediately to multiple regression; the only difference is that in the multiple regression case ^Yi will be calculated using several independent variables instead of one, and the degrees of freedom (see later) will be adjusted accordingly.

    1.  Predictor and Residual

    As presented earlier the regression model implies that for each observation in the sample (see previous exhibit)
    Yi  = ^Yi  + ei   i=1,...,n
    where
    ^Yi  =  b0 + b1Xi
    is the predictor (or fitted value, or estimate) of Yi  given Yi, and
    ei  = Yi  - ^Yi
    is called the residual.
    Note that Yi , ^Yi , and ei  are all measured on the same vertical axis.

    2.  Partitioning Sum of Squares Total

    The principle of ANOVA is shown in the next figure. From the figure, one can see that the total variation of Yi from the sample mean of Y, (yi - y.), can be decomposed into two components:
     
    yi - y.
    =
    ^yi - y.
    +
    yi - ^yi
    (total deviation of Yi from mean)
    (deviation of fitted value from mean)
    (deviation of Yi from fitted value)

    Next take the sum of the squares of each deviation over all observations in the sample.
     

    Sum of squares:
    S(Yi - Y.)2
    S(^Yi - Y.)2
    S(Yi - ^Yi)2
    Name:
    SSTO for sum of squares total
    SSR for sum of squares regression
    SSE for sum of squares error
    Meaning:
    (total variation in Y)
    (variation in Y accounted for by regression line)
    (variation in Y around regression line)

    SSE is also called residual sum of squares.  The basic ANOVA result (or theorem) is that the sums of squared deviations stand in the same relation as the (unsquared) deviations, so that:
     

     
    S(Yi - Y.)2
    =
    S(^Yi - Y.)2
    +
    S(Yi - ^Yi)2
    or
    SSTO
    =
    SSR
    +
    SSE

    This is actually a remarkable and non-obvious property that must be proven!  (See optional proof in ALSM5e p. <>.)  Table 3 shows the calculations of ANOVA sums of squares for the regression of % clerks (Y) on employment seasonality (X).
     
    Table 3.  Calculations for ANOVA Sums of Squares
    i
    Sector
    Xi
    Yi
    ^Yi
    ei
    		 (Yi - Y.)2 (^Yi - Y.)2 (Yi - ^Yi)2
    1 STRSEW 73 4.8 2.311 2.489 9.958 31.856 6.193
    2 SAND 43 7.6 7.374 0.226 0.126 0.338 0.051
    3 VENT 29 11.7 9.737 1.963 14.021 3.173 3.854
    4 BRICK 47 3.3 6.699 -3.399 21.674 1.578 11.555
    5 GENCON 43 5.2 7.374 -2.174 7.593 0.338 4.727
    6 SHEET 29 11.7 9.737 1.963 14.021 3.173 3.854
    7 PLUMB 20 10.9 11.256 -0.356 8.670 10.891 0.127
    8 ELEC 13 12.5 12.437 0.063 20.652 20.084 0.004
    9 PAINT 59 3.9 4.674 -0.774 16.448 10.768 0.599
    Total 356 71.6 113.162 82.199 30.963
    Mean 39.556 7.956
    = SSTO
    = SSR
    = SSE
    b1 = -0.169
    b0 = 14.631

    Alternative computational formulas are:

    3.  Partitioning of Degrees of Freedom

    To each sum of squares correspond degrees of freedom (df).  Degrees of freedom are additive.
     
     
    n - 1
    =
    1
    +
    (n - 2)
    df for SSTO
    df for SSR
    df for SSE
    (1 df lost estimating Y.)
    (1 df lost estimating b1)
    (2 df lost estimating
    b0 and b1)

    4. Mean Squares

     Mean squares are the sums of squares divided by their respective df.  Mean squares are not additive.
     
    SSTO/(n - 1)
    SSR/1
    SSE/(n - 2)
    s2(Y) = mean squares y or
    sample variance of y
    MSR = mean squares regression
    MSE = mean squares error

    Mean squares total is simply the sample variance of Y.
    MSE is an estimate of the variance of the residuals s2.

     5. ANOVA Table

    The ANOVA table summarizes all this information.  Table 4a shows the ANOVA table in symbolic form.
     
    Table 4a.  ANOVA Table in Symbolic Form
    Source Sum of Squares df Mean Squares F-ratio
    Regression SSR   1 MSR=SSR/1 F*=MSR/MSE
    Error SSE n-2 MSE=SSE/(n-2)
    Total SSTO n-1 s2{Y}=SSTO/(n-1)

    Table 3b shows the ANOVA table for the regression of % clerks on employment seasonality.
     
    Table 4b.  ANOVA Table for Construction Industry Data
    Source Sum of Squares df Mean Squares F-ratio
    Regression 82.199   1 82.199 18.583
    Error 30.963 7 4.423
    Total 113.162 8 14.145

    The F-ratio is calculated as the ratio F* = MSR/MSE (here 82.199/4.423 = 18.583); the meaning of F* is discussed in Module 2.

    Q - What are the meanings of the quantities 4.423 and 14.145 in Table 3?

    The ANOVA table is part of the usual regression output.

    7.  (Optional) Derivation of ANOVA Relation SSTO = SSR + SSE

    See ALSM5e p. <>.
     

    8.  Measures of Association: Coefficients of Determination & Correlation

    1.  Coefficient of Determination (R-squared)

    The following formulas are equivalent:
    r2 = (SSTO - SSE)/SSTO = SSR/SSTO = 1 - SSE/SSTO
    where 0 <= r2 <= 1

    Example: In the regression of % clerks on seasonality the r2 can be calculated equivalently as

    (113.162 - 30.963)/113.162 = 82.199/113.162 = 1 - (30.963/113.162) = 0.726
    Limiting cases: It is customary to interpret r2 as the proportion of the variation in y "explained" by the regression model.  But note that "variation" refers to the sum of squared deviations, so variation is measured in squared units, not original units of y, so interpretation of r2 as explained variation is not entirely intuitive.  An alternative substantive interpretation focuses on the standardized regression coefficient b1* (explained later).

    2.  Coefficient of Correlation

    The following formulas are equivalent derivations of the correlation coefficient r:
    1. r = +/- (r2)1/2
    2. r = (S(Xi - X.)(Yi - Y.))/((S(Xi - X.)2S(Yi - Y.)2)1/2
    3. r = sXY/(sXsY)
    In the first formula the expression "+/-" means that r takes the sign of b1.  Thus r can be thought of as the positive square root of the r2, associated with the same sign as the slope b1.  The third formula expressing r as the ratio of the covariance of X and Y divided by the product of the sample standard deviations of X and of Y is equivalent to the second one; since the numerator and denominator of the second formula are each divided by (n - 1), the divisor cancels out.
    When r2 is not 0 or 1,
    |r| > r2
    so that the absolute value of r is always larger than r2.  Thus r suggests a stronger relationship and thus has a greater psychological impact than that of r2.  An example is the regression of % clerks on seasonality where the r2 is 0.726 and the correlation coefficient r is a more impressive -.852.

    Examples of the degree of association corresponding to various values of r are shown in the next exhibit.

    The correlation coefficient r alone can give a misleading idea of the nature of a statistical relationship, so it is important to always look at the scatterplot of the relationship.

    3.  Standardized Regression Coefficient

    1.  Calculation
    The standardized regression coefficient  b1* is  calculated as:
    b1*  =  b1(sX/sY)
    i.e., b1* is equal to b1 multiplied by the standard deviation of X and divided by the standard deviation of Y.  Thus in the simple linear regression model the standardized regression coefficient is the same as the correlation coefficient:
    b1* = (sXY/sX2)(sX/sY) = sXY/(sXsY) = r
    but this is no longer true in the multiple regression model.
    Conversely, recover the unstandardized regression coefficient b1 from the standardized coefficient b1* as
    b1  =   b1*(sY/sX)   ( = r(sY/sX), in simple linear regression only)
    where sX and sY are the sample standard deviations of X and Y, respectively.

    In the construction industry study the regression coefficient b1 is -.169; the standard deviations of X and Y are 18.994 and 3.761, respectively.  Thus the standardized coefficient of seasonality is -.169(18.944/3.761) = -.852.  Thus an increase of in SD in X is associated with a decrease of .852 SD deviation of Y.  (The standardized coefficient can also be automatically computed by the statistical program.)

    Standardized coefficients are found in many statistical contexts, including multiple regression models and structural equations models.  Calculating the standardized coefficient from the unstandardized coefficient, and vice-versa, is always done the same way.  Suppose the unstandardized coefficient b of the regression of a variable Y on a variable X is represented as

    X -- b --> Y
    Then It always works, even in the most complicated situations!  (Loehlin 2004, p. ??).
    2.  Interpretation
    b1* measures the change in ^y, measured in units of standard deviation of y, associated with a one standard deviation increase in x.
    Example: Brody (1992: 253) reports a correlation of .57 between 6th grade IQ test score and the number of years of education that a person obtained.  One can interpret this correlation as a standardized regression coefficient: b* = .57 means that an individual with a 6th grade IQ score 1 SD above the mean would be expected to obtain .57 SD years of education above the mean.
    The following picture shows an interpretation of b1* as a shift along distribution of years of education caused by a positive shift of 1 SD of IQ from the mean. Standardized coefficients are especially useful in the multiple regression model, where they permit comparing the relative magnitudes of the coefficients of independent variables measured in different units (such as a variable measured in years, and another measured in thousands of dollars).

    9.  Data for Regression Analysis & Causal Interpretation

    In current usage the term data is used either as a collective in the singular ("data is") or as the plural of datum ("data are").

    Data for regression analysis comes from two kinds of sources.

    1. Observational data are data obtained from nonexperimental studies so that values of X are not controlled.  An example is life expectancy of countries as a function of literacy.  Observational data do not directly offer strong support for causal interpretations.
    2. Experimental data are measured from experimental units that are randomly assigned to treatments, i.e., different values of the independent variable(s) X set by the experimenter.  Experimental data allow stronger causal inferences.

    Compare the following two studies with respect to the strength of causal inference.

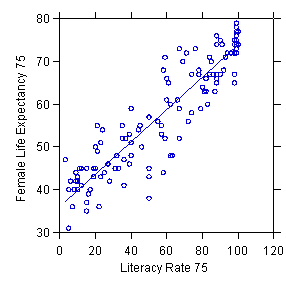
    Example of observational data: Regression of female life expectancy on literacy rate for countries

    Estimated regression:  Y = 36.212 + .377X     R2=.844  N=131

    Example of experimental data: Shepard's experiment

    "The data are from a perceptual experiment in which subjects viewed pairs of objects differing only by rotational angle.  [...]  The rt variable is reaction time (delay in saying "same" for a pair).  [...]  Shepard's remarkable discovery in this and other experiments was that the rotational angle is linearly related to reaction time.  The February 19, 1971 cover of Science magazine displayed five of Shepard's computer-generated images under various rotations.  This research has been replicated by psychologists and neuroscientists studying spatial processing in humans and other primates.  Shepard received the National Medal of Science for this and other work in cognitive psychology."  (Wilkinson 1999, p. 337.)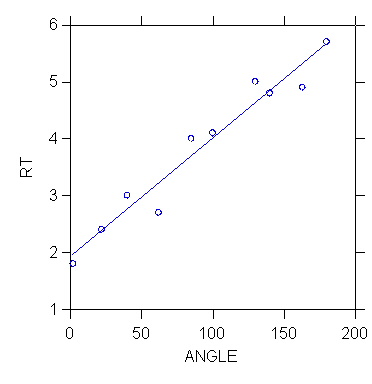

     
    Estimated regression:  RT = 1.916 + (.021)ANGLE      R2 = .949   N=10

    10.  Historical Note

    1.  The Method of Least Squares

    The method of least squares (French "moindres carrés") was developed by Adrien Legendre (1752-1833) in the context of reconciling astronomical observations; it was first published in 1805.  Try your French on Legendre's appendix below (but be aware today's notation is different from Legendre's).

    2.  The Idea of Regression and Correlation

    The idea of regression and correlation (and the term regression) is attributed to British polymath-genius Francis Galton (1822-1911), a cousin of Charles Darwin.  The term regression originated in the regression of the height of sons regressed on the height of fathers; the height of sons exhibits a "regression to mediocrity" (i.e., toward the mean of the population).

    11.  Simple Linear Regression in Practice

    1.  SYSTAT Examples

    >USE "Z:\mydocs\ys209\sexdipri.syd"
    SYSTAT Rectangular file Z:\mydocs\ys209\sexdipri.syd,
    created Tue Apr 23, 2002 at 08:35:28, contains variables:
     SPECIES$     LENGTHDI     WEIGHTDI     MEANHARE     MAXHARE

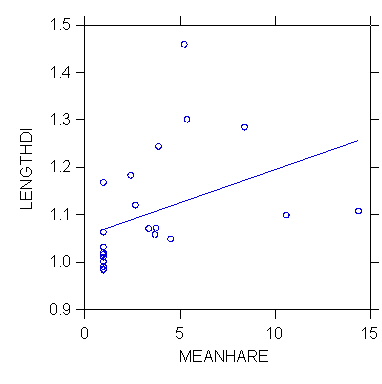
    >rem relationship berween sex dimorphism (length ratio male to female) and
    >rem mean harem size in primates, a measure of sexual competition among males
    >rem ask me for the whole bizarre story
    >regress
    >model lengthdi=constant+meanhare
    >estimate

    Dep Var: LENGTHDI   N: 22   Multiple R: 0.403   Squared multiple R: 0.162

    Adjusted squared multiple R: 0.120   Standard error of estimate: 0.115

    Effect         Coefficient    Std Error     Std Coef Tolerance     t   P(2 Tail)
    CONSTANT             1.055        0.035        0.000      .      29.949    0.000
    MEANHARE             0.014        0.007        0.403     1.000    1.967    0.063

    Analysis of Variance
    Source             Sum-of-Squares   df  Mean-Square     F-ratio       P

    Regression                 0.051     1        0.051       3.870       0.063
    Residual                   0.266    20        0.013

    -------------------------------------------------------------------------------
    *** WARNING ***
    Case           17 has large leverage   (Leverage =        0.487)
    Case           19 is an outlier        (Studentized Residual =        3.821)

    Durbin-Watson D Statistic          1.949
    First Order Autocorrelation       -0.026

    >plot lengthdi*meanhare/stick=out smooth=linear short


     
     

    >USE "Z:\mydocs\ys209\yule.syd"
    SYSTAT Rectangular file Z:\mydocs\ys209\yule.syd,
    created Wed Feb 17, 1999 at 09:34:32, contains variables:
     UNION$       PAUP         OUTRATIO     PROPOLD      POP

    >model paup=constant+outratio
    >estimate

    Dep Var: PAUP   N: 32   Multiple R: 0.594   Squared multiple R: 0.353
    Adjusted squared multiple R: 0.331   Standard error of estimate: 13.483

    Effect         Coefficient    Std Error     Std Coef Tolerance     t   P(2 Tail)
    CONSTANT            31.089        5.324        0.000      .       5.840    0.000
    OUTRATIO             0.765        0.189        0.594     1.000    4.045    0.000

    Analysis of Variance
    Source             Sum-of-Squares   df  Mean-Square     F-ratio       P
    Regression              2973.751     1     2973.751      16.359       0.000
    Residual                5453.468    30      181.782

    -------------------------------------------------------------------------------
    *** WARNING ***
    Case           15 has large leverage   (Leverage =        0.328)

    Durbin-Watson D Statistic          1.853
    First Order Autocorrelation       -0.018


     

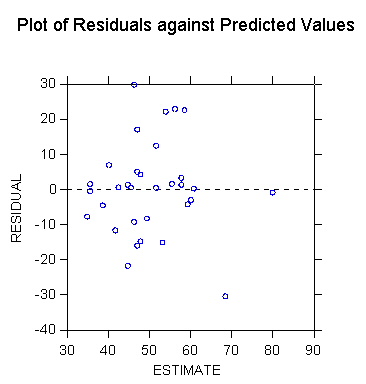
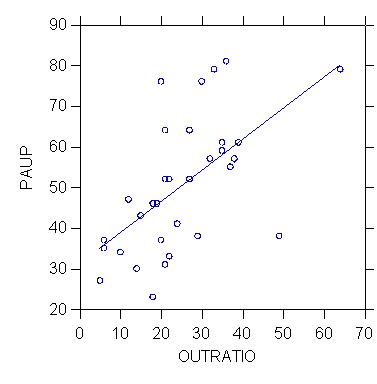
    >plot paup*outratio/stick=out smooth=linear short


     
     

    2. STATA Examples

    . set mem 32000
    (32000k)

    . use "Z:\mydocs\S208\gss98.dta", clear

    . su income

        Variable |     Obs        Mean   Std. Dev.       Min        Max
    -------------+-----------------------------------------------------
          income |    2699    10.85624   2.429604          1         13

    . su  educ

        Variable |     Obs        Mean   Std. Dev.       Min        Max
    -------------+-----------------------------------------------------
            educ |    2820    13.25071   2.927512          0         20

    . regress income educ

          Source |       SS       df       MS              Number of obs =    2688
    -------------+------------------------------           F(  1,  2686) =  235.66
           Model |  1269.91329     1  1269.91329           Prob > F      =  0.0000
        Residual |  14474.0495  2686  5.38870049           R-squared     =  0.0807
    -------------+------------------------------           Adj R-squared =  0.0803
           Total |  15743.9628  2687  5.85930882           Root MSE      =  2.3214

    ------------------------------------------------------------------------------
          income |      Coef.   Std. Err.      t    P>|t|     [95% Conf. Interval]
    -------------+----------------------------------------------------------------
            educ |   .2359977   .0153731    15.35   0.000     .2058533    .2661421
           _cons |    7.71967   .2094621    36.85   0.000     7.308947    8.130393
    ------------------------------------------------------------------------------
     
     


    Last modified 9 Jan 2006