All the Tests You Will Ever Need to Do With Simple Regression

This example is based on the regression analysis by Yule (1899) of the change in the poverty rate in British unions (= districts) (PAUP) as a function of change in the proportion of out-relief (= poverty relief given outside of the poorhouses) (OUTRATIO).


Dep Var: PAUP   N: 32   Multiple R: 0.594032   Squared multiple R: 0.352875

Adjusted squared multiple R: 0.331304   Standard error of estimate: 13.482665

Effect         Coefficient    Std Error     Std Coef Tolerance     t   P(2 Tail)

CONSTANT         31.089437     5.323809     0.000000   .        _______  _______
OUTRATIO          0.765389     0.189237     0.594032  1.000000  _______  _______

                             Analysis of Variance

Source             Sum-of-Squares   df  Mean-Square     F-ratio       P

Regression           2973.750962     1  2973.750962   __________    _________
Residual             5453.467788    30   181.782260
-------------------------------------------------------------------------------

*** WARNING ***
Case           15 has large leverage   (Leverage =     0.328486)

Durbin-Watson D Statistic     1.853
First Order Autocorrelation  -0.018



Do the following tests (use a = .05, confidence = .95):
 

1.  Test hypothesis that b1 <> 0
 

2.  Test hypothesis that b1 <>  0.5
 

3.  Test hypothesis that b1 > 0
 

4.  Calculate a CI for b1
 

5.  Do the equivalent of 1, 2 (b0 <> 20), 3, and 4 for b0
 

6.  F test of the significance of the entire regression model (overkill in a simple regression but useful in multiple regression)
 

7.  CI for the mean response ^Yh (for a single ^Yh)
 

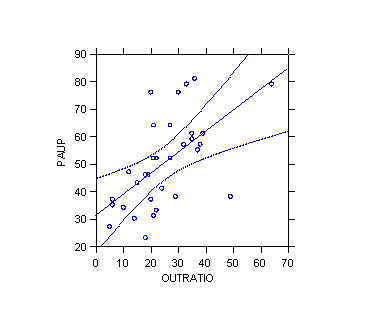
8.  CI for the mean response for several ^Yh: Working-Hotelling confidence band (see picture)
 

9.  Prediction interval for Yh(new)
 
 


Last modified 8 Feb 2000