SOCI209 - Module 2 - INFERENCE IN SIMPLE LINEAR REGRESSION

1.  Inference in Regression Models

From Module 1 the parameters b1 and b0 are estimated as
b1 = (S(Xi - X.)(Yi - Y.))/S(Xi - X.)2
b0 =  Y.- b1X.
Just like other statistics (such as the sample mean or variance) the estimates b1 and b0 are functions of the observed values Yi, which are functions of the random errors ei.  Thus b1 and b0 are themselves random variables and b1 and b0 each has a probability distribution, called the sampling distribution.  The sampling distribution of b1 (respectively b0) refers to "the different values of b1 (b0) that would be obtained with repeated sampling when the levels of the independent variables X are held constant from sample to sample" (ALSM5e p. 41; ALSM4e p. 45).  Statistical inference concerning populations parameters such as b1 and b0 consists in testing hypotheses and constructing confidence intervals for that parameter.  Inference concerning a parameter is based on the sampling distribution of that parameter.

For (simple or multiple) linear regression models statistical inference is commonly carried out for

  1. the regression coefficients  b1 and b0 (hypothesis tests and confidence intervals)
  2. the mean response E{Yh} knowing Xh (whether Xh corresponds or not to an observation in the sample) (confidence intervals only)
  3. the individual value of a "new" observation Yh(new) knowing Xh (whether Xh corresponds or not to an observation in the sample) (confidence intervals only)
  4. F test of the significance of the regression model as a whole (test only)

2.  Inference on b1 and b0

1.  Sampling Distribution of b1

The informal derivation below shows that if the errors ei are normally distributed the sampling distribution of t*=(b1- b1)/s{b1} is a Student t distribution with (n-2) degrees of freedom (df).  t* refers to the deviation (b1- b1) of b1 from its expectation (b1) divided by the estimated standard error s{b1} of b1 (i.e., the estimated standard deviation of the sampling distribution of b1).   The standard error s{b1} is estimated from the data as s{b1}=[MSE/S(Xi - X.)2 ]1/2.  Thus t is the standardized value of b1 (i.e., a z-score).  When the distribution of errors is not too far from normal and the sample is not too small the distribution of t approximately follows a Student t distribution.  Even when the distribution of errors is far from normal, the distribution of t* approaches a Student t distribution (actually a normal distribution) as the sample size n becomes large.
  
Informal derivation of the sampling distribution of t*

  
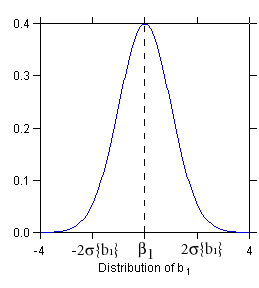
STEP 1: Sampling Distribution of b1
Assuming that errors are normally distributed
b1  ~ N ( b1 , s2{b1})   (~ means is distributed as)
where s2 denotes the variance of ei and s2{b1} = s2 / S(Xi - X.)2.  In words: b1 is normally distributed with mean  E{b1} = b1 and variance s2{b1} = s2 / S(Xi - X.)2 (figure at left).

The sampling distribution of b1 is normal because b1 is a linear combination of the observations Yi which are independent normally distributed random variables (ALSM5e, ALSM5e: Appendix A, Theorem A.40).  Note the denominator S(Xi - X.)2  in the expression for s2{b1}: the greater the variance of X, the smaller the variance s2{b1} of the sampling distribution, and the more precise the estimation of b1.  (In experimental research, where the experimenter sets the values of X, one may be able to space the X values optimally to achieve the smallest s2{b1} possible.)
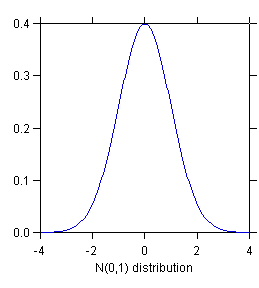Distribution of (b1-b1)/ s{b1}
STEP 2: Distribution of (b1-b1)/s{b1}
(b1-b1)/s{b1} ~ N (0, 1)
In words: the deviation of b1 from its mean b1 , divided by the standard error s{b1}, is normally distributed with mean 0 and standard deviation 1 (i.e., according to a standard normal distribution).  This follows from STEP 1 by applying to b1 by the equivalent of the z transformation z = (X - m)/s.
s{b1} denotes the standard deviation of the sampling distribution of b1.  s{b1}  is called the standard error of b1.
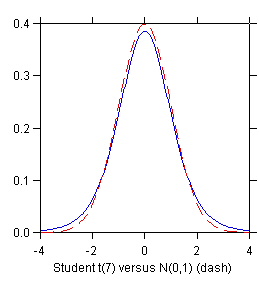Distribution of t* = (b1- b1)/ s{b1}  (solid
blue line) compared to distribution of 
(b1- b1)/ s{b1}  (red dashed line)
STEP 3: Distribution of (b1 -  b1)/ s{b1}
In practice s{b1} is not known (because s is not known) so one replaces the standard error s{b1} with the sample estimate s{b1} given by
s{b1} = [MSE / S(Xi - X.)2]1/2
where MSE is the mean squares error.  When s{b1} is replaced by the sample estimate s{b1}, the sampling distribution is no longer normal.  It becomes a Student t distribution with (n-2) df: 
t* = (b1- b1)/ s{b1} ~ t (n - 2)
The distribution is no longer normal because s{b1} (being a sample estimate) is a random variable rather than a fixed constant. This "extra randomness" produces the thicker tails of the t distribution compared to the normal.  The (n - 2) df correspond to the (n - 2) df of MSE (see Module 1). 

 
The derivation of the sampling distribution of b0 is shown later.

Inference on the regression coefficients uses the following formulas.
 
Table 1.  Formulas for Inference on b1 and b0
Slope b1  
Estimated standard error of b1 s{b1} = (MSE/S(Xi - X.)2)1/2
Estimated sampling distribution of b1 (b1 - b1)/s{b1} ~ t(n - 2) 
Confidence limits for CI on b1 b1 +/- t(1 - a/2; n - 2)s{b1}
Test statistic for H0: b1 = b10 t* = (b1 - b10)/s{b1} (1)
Intercept b0  
Estimated standard error of b0 s{b0} = (MSE(1/n+X.2/S(Xi - X.)2)1/2
Estimated sampling distribution of b0 (b0 - b0)/s{b0} ~ t(n - 2) 
Confidence limits for b1 b0 +/- t(1 - a/2; n - 2)s{b0}
Test statistic for H0: b0 = b00 t* = (b0 - b00)/s{b0}  (1)
Notes: (1)
  • b10 and  b00 denote hypothetical values of the parameters      
  • when b10 = 0 (the most common type of hypothesis) then t* = b1/s{b1}

The estimated standard error s{b1} is typically provided in the standard regression printout (labeled Std Error in Table 2).

Table 2 repeats the regression printout used for illustration.

Table 2.  Printout of Regression of % Clerks on Seasonality Index


Dep Var: CLERKS   N: 9   Multiple R: 0.852   Squared multiple R: 0.726

Adjusted squared multiple R: 0.687   Standard error of estimate: 2.103

Effect         Coefficient    Std Error     Std Coef Tolerance     t   P(2 Tail)

CONSTANT            14.631        1.700        0.000      .       8.607    0.000
SEASON              -0.169        0.039       -0.852     1.000   -4.311    0.004

Analysis of Variance
Source             Sum-of-Squares   df  Mean-Square     F-ratio       P

Regression                82.199     1       82.199      18.583       0.004
Residual                  30.963     7        4.423

2.  Inference on b1

We look at inference on b1 first because it is the most common.
Confidence Interval for b1
From Table 1 the confidence limits of the CI for b1 are
b1 +/- t(1 - a/2; n - 2)s{b1}
where t(1 - a/2; n - 2) refers to the (1 - a/2)100th percentile of the Student t distribution with (n-2) df.
Example: find the 95% CI for b1, the coefficient of seasonality in the simple regression of % clerks.
b1 = -.169 (from regression printout under Coefficient)
s{b1} = .039 (from regression printout under Std Error)
choose a = .05; then t(1-a/2; n-2) = t(.975; 7) = 2.365 (from statistical program or from table)
Therefore the 95% CI for b1 is
L = -.169 - (2.365)(.039) = -0.261 (lower bound of CI)
U = -.169 + (2.365)(.039) = -0.077 (upper bound of CI)
One can say that with 95% confidence
-0.261 <= b1 <= -0.077
Two-sided test for b1
Example: Test the hypothesis that the coefficient of seasonality b1 = 0.  The setup is The test statistic corresponding to H0: b1 = 0 is
t* = (b1 - 0)/s{b1} = b1/s{b1}
(provided in the regression printout under t).

Choose a significance level a = .05.

Using the P-value approach, the test statistic is

t* = (-.169)/(.039) = -4.311 (also from regression printout under t)
Find the 2-tailed P-value
P{|t(n - 2)| > |t*| = 4.311 = .004 (from regression printout under P(2 Tail)).
Since P-value = .004 < a = .05, one concludes H1, that "there is a significant linear association between % clerks and seasonality", or "the coefficient of seasonality is significant at the .05 level".  (One would actually say "at the .01 level" in this case, choosing the lowest "round" significance level greater than the P-value .004.)

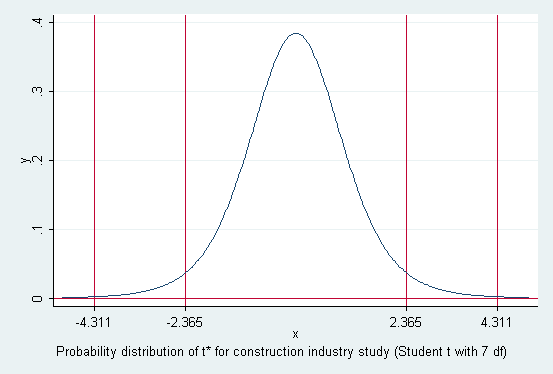
Using the decision theory method the decision rule is

if |t*| <= t(1-a/2; n-2), conclude H0
if |t*| > t(1-a/2; n-2), conclude H1
With a = .05, t(1-a/2; n-2) is
t (0.975; 7) = 2.365
Since |t*| = 4.311 > 2.365 conclude H1 (b1<> 0) at the .05 level with this method also.
One-sided test for b1
Hint: It is often easier to write down H1 (the "research hypothesis") first; then H0 is the complement of H1
In the regression of % clerks on seasonality the one-sided test is lower-tailed, since b1 (-.169) is negative, so the hypothesis setup is To carry out the test In the example the 2-sided P-value is .004; thus the 1-sided P-value is
P(t(n - 2) < t*) = (.004)/2 = .002
Since P-value = .002 < .05 = a, conclude H1: b1 < 0.

Using the decision theory method the decision rule is

if |t*| <= t(1-a; n-2), conclude H0
if |t*| > t(1-a; n-2), conclude H1
In the example
t(1-a; n-2) = t(0.95; 7) = 1.895
Since |-4.311| > 1.895, conclude H1:  b1 < 0 by this method also.
Comparing Two-sided and One-sided Tests for b1
Comparing the two types of tests it appears that the 1-sided test is "easier" (i.e., more likely to turn up significant) than the corresponding 2-sided test.  (For example, the P-value of the 1-sided test is half the P-value of the 2-sided test.)
Thus there is an incentive to use 1-sided tests to increase the chance of significant results.  It is considered legitimate to use a 1-sided test whenever one has a genuine directional hypothesis concerning b1.  In the construction industry study the author's expectation that greater seasonality is associated with less bureaucracy (implying a negative slope) is a genuine directional hypothesis.  Thus a 1-sided test is appropriate in this case.  (In any case in this example the slope is significant in the 2-sided test, too.)  This opinion on the use of one-tailed tests is widely shared by reviewers of professional journals.  However, some statisticians recommend using 2-sided tests exclusively, on the ground that the 2-sided test is conservative.

3.  Inference on b0

CIs and tests for b0 are carried out in exactly the same way as for b1.
Q - Using information from the printout

4.  (Optional) Sampling Distribution of b0

The intercept b0 is estimated as
b0 = Y. - b1X.
The estimated standard error of b0 is
s{b0} = (MSE(1/n+X.2/S(Xi - X.)2)1/2
The standardized statistic
t* = (b0 - b0)/s{b0} is distributed as t(n - 2)
(See ALSM5e pp. 48-49; ALSM4e pp. <>)

3.  Inference for Mean Response E{Yh}

1.  Sampling Distribution of ^Yh

The mean response  E{Yh} is estimated as ^Yh = b0 + b1Xh.  Thus the variance of the sampling distribution of ^Yh is affected by variance in both  b0 and b1 sampling and by how far Xh is from the sample mean of X.  The way in which the variance of ^Yh depends on the distance of Xh from X. is shown in the next exhibit: given a change in b1, the change in ^Yh is larger further away from the mean.
Table 3.  Formulas for Inference on ^Yh
Point estimator of E{Yh} ^Yh = b0 + b1Xh
Estimated standard error of ^Yh s{^Yh} = (MSE ((1/n) + (Xh - X.)2 / S(Xi - X.)2))1/2
Estimated distribution of ^Yh (^Yh - E{Yh}) / s{^Yh} ~ t (n-2) 
Confidence limits for CI on E{Yh} ^Yh +/-  t(1- a/2; n-2)s{^Yh}
Test statistic  Not often used
Notes:
  • Xh is a given level of X which does not necessarily correspond to a data point Xi
  • the standard error of ^Yh is affected by (Q - explain how)
    • MSE
    • (Xh - X.) the deviation of Xh from the sample mean of Xi
    • variability of Xi
    • sample size n

2.  CI for Mean Response E{Yh}

Example 1
Given the regression of % clerks on seasonality, calculate an interval estimate for E{Yh} when seasonality is 35, i.e. Xh = 35.
First calculate s{^Yh}.
From the regression printout in Table 2 n = 9 and MSE = 4.423.
One needs additional information not contained in the standard regression output.
From Module 1, Table 1: X. = 39.556; S(Xi - X.)2 = 2886.222.
For Xh = 35, ^Yh = 14.631 + (-0.169)(35) = 8.716 and (Xh - X.)2 = (35 - 39.556)2 = 20.757.
Thus s{^Yh} = (4.423((1/9) + 20.757/2886.222))1/2 = 0.7233628.
Choose a = .05, so that t(.975;7) = 2.365.
Then the confidence limits for E{Yh} are
L = 8.716 - (2.365)(0.7233628) = 7.005  (lower bound)
U = 8.716 + (2.365)(0.7233628) = 10.427  (upper bound)
so that with 95% confidence
7.005 <= E{Yh|Xh = 35} <= 10.427
Example 2
This example illustrates a technique to obtain s{^Yh} from the computer rather than computing it "by hand".
The example uses the data set knnappenc07.syd (see KNN Appendix C data set 07).  Units are 522 home sales in a mid-western town.  Y is the sale price in dollars; X is the finished area of the home in square feet.  The county tax collector runs a simple regression of sale price on finished area, obtaining
^Y = -81432.9464 + 158.9502X  n=522  R2 = .6715
The tax collector wants to estimate of the average sale price (i.e., E{Yh}) of homes with 2,500 square feet of finished area and obtain a 95% CI for that average sale price.  To calculate both ^Yh and s{^Yh} quickly, the tax collector adds a 523d "dummy" case to the data set, with only the value of 2500 for X and missing value for Y and re-runs the regression.  Then he obtains  ^Yh and s{^Yh} for all observations, including the dummy one (STATA predict yhat, xb; predict seyhat, <>; SYSTAT save resid with variables ESTIMATE and SEPRED).
So for Xh=2500
^Yh =  315942.6306
s{^Yh} = 3654.4390
Thus using the formula above the 95% CI for the average sale price of homes with 2,500 square feet of finished space is
L = 315942.6306 - (1.9645365)(3654.4390) = 308763.35  (lower bound)
U = 315942.6306 + (1.9645365)(3654.4390) = 323121.91  (upper bound)
Note that this is a relatively narrow interval, indicating that the average sale price of 2500 square feet homes can be estimated quite precisely.

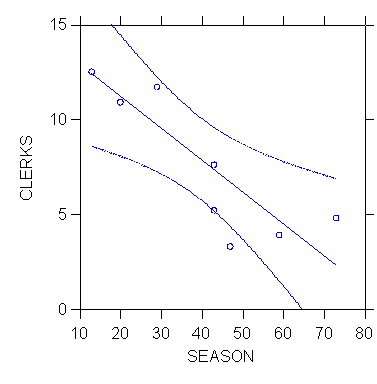
3.  CI for the Entire Regression Line - the Working-Hotelling Confidence Band

The Working-Hotelling confidence band is a CI for the entire regression line E{Y} = b0+b1X.  The next exhibit shows the 95% Working-Hotelling confidence band for the regression of % clerks on seasonality.  The W-H confidence band is often examined graphically. The bounds of the (1-a) W-H confidence band for Xh are given by
^Yh +/- Ws{^Yh}
where
W = [2F(1-?; 2, n-2)]1/2
(See ALSM5e pp. 61-63.)

4.  (Optional) Derivation of Sampling Distribution of ^Yh

The standard error of ^Yh is estimated as
s{^Yh} = (MSE ((1/n) + (Xh - X.)2 / S(Xi - X.)2))1/2
(^Yh - E{Yh})/s{^Yh} is distributed as a t distribution with (n-2) df.  (See ALSM5e pp. 52-54.)

4.  Prediction Interval for a New Observation Yh(new)

1.  Sampling Distribution of Yh(new)

Prediction intervals are especially important for quality control (QC) in an industrial context.  (The procedure is explained in detail in ALSM5e pp. 55-61; ALSM4e pp. 61-66 pp. 61-66.)

Examples:

In both cases one is trying to predict the value Yh(new) of the response for an individual case with a specific value Xh of the independent variable.  This is different from the previous situation where one wants to estimate the average value of Y for X=Xh.
One estimates Yh(new) as ^Yh,= b0+b1Xh, the value of ^Y on the regression line corresponding to Xh.
Variation in Yh(new) is affected by two sources: The decomposition of the variation in Yh(new) is shown in the next two exhibits. Therefore,
s2{Yh(new)} = s2 + s2{^Yh}
Thus the sampling disribution of Yh(new) is described as in the following table.
 
Table 4.  Formulas for Inference on Yh(new)
Point estimator of Yh(new) ^Yh = b0 + b1Xh
Estimated standard error s{Yh(new)}  (s{pred}) s{pred} = (MSE (1 + (1/n) + (Xh - X.)2 / S(Xi - X.)2 ))1/2
Estimated distribution of Yh(new) (Yh(new)  - E{Yh}) / s{pred} ~ t (n-2) 
Confidence limits for CI on Yh(new) ^Yh +/-  t(1- a/2; n-2)s{pred}
Test statistic  Not often used

2.  CI for  Yh(new)

This example uses again the SYSTAT data set knnappenc07.syd (see KNN Appendix C data set 07).  Units are 522 home sales in a mid-western town.  Y is the sale price in dollars; X is the finished area of the home in square feet.  The estimated regression is
^Y = -81432.9464 + 158.9502X  n=522  R2 = .6715
Imagine this time that that someone plans to sell their home in this Midwestern town.  They ask a real-estate agent to estimate the price the home might fetch on the market, given that it has 2500 square feet of finishes space, and to give them a 95% CI for that price.  The real estate agent uses the same trick as the tax collector, of adding a "dummy" 523d case with X = 2500 to obtain both ^Yh and s{^Yh}; she also obtains MSE from the regression printout, so she has the following information
^Yh = 315942.6306
s{^Yh} = 3654.4390
MSE = 6.26043E+09
From this information she calculates s2{Yh(new)} as
s2{Yh(new)} = s2 + s2{^Yh} = MSE + (SEPRED)2 = 6.26043E+09 + (3654.4390)2 = 6273784924.40
Hence s{Yh(new)} = (6273784924.40)1/2 = 79207.23.
Thus the 95% CI for the estimated sale price of an individual 2500 square feet home is obtained as
L = 315942.6306 - (1.9645365)(79207.23) = 160337.14  (lower bound)
U = 315942.6306 + (1.9645365)(79207.23) = 471548.12  (upper bound)
Note that the 95% CI for Yh(new) (160K to 472K) is considerably wider than the CI for the mean response E{Yh} (309K to 323K).  (Q - Why is that?)

3.  (Optional)  Derivation of Sampling Distribution of  Yh(new)

See ALSM5e pp. 55-60.

5.  F Test for Entire Regression (Alternative Test of b1 = 0)

1.  F Test of b1 = 0

Here this test is overkill, since the t test can be used to test the hypothesis that b1 = 0.
But the F test generalizes to multiple regression to test the hypothesis that all the regression coefficients are zero.

2.  Expected Mean Squares

One can show that
E{MSE} = s2
E{MSR} = s2 + b12 S(Xi - X.)2
(ALSM5e pp. 68-71; ALSM4e pp. 75-76)

Note that if  b1=0, E{MSR} = E{MSE} = s2.
Therefore, an alternative to the 2-sided hypothesis test for b1

H0: b1 = 0
H1: b1 <> 0
is the F test
F* = MSR/MSE
If b1 = 0, E{F*} = s2/s2  = 1.
If b1<> 0, E{F*} > 1.
Thus the larger F*, the more likely that b1 <> 0.
It can be shown that if H0 holds (i.e., if b1=0)
F* = MSR/MSE ~ (c2(1)/1 ) / (c2(n-2)/(n-2)) = F(1; n-2)
(ALSM5e p. 70;  ALSM4e pp. 76-77)

3.  Carrying Out the F Test

Example: Carry out the F test for the regression of % clerks on seasonality.
Choose a = .05.
Using the P-value method, calculate F* as
F* = MSR/MSE = (82.199)/(4.423) = 18.583
The P-value is P{F(1;7) > 18.583} = 0.004.
Since P-value = 0.004 < .05 = a, conclude H1: b1 <> 0.
Using the decision theory method, the decision rule is
if F* <= F(1-a ; 1, n-2), conclude H0
if F* > F(1-a ; 1, n-2), conclude H1
F(1-a ; 1, n-2) = F(0.95;1,7) = 5.59.
Since F* = 18.583 > 5.59, conclude H1: b1 <> 0 by this method also.
The principle of the decision theory method is shown in the next exhibit.

4.  Equivalence of t Test and F Test

In the simple linear regression model, F* = (t*)2.
Example: In the regression of % clerks on seasonality, the squared t-ratio for b1 is equal to F*, i.e.
(t*)2 = (-4.311)2 = 18.583 = F*
This is no longer true in the multiple regression model.

6.  Maximum Likelihood Estimation

When the functional form of the probability distribution of ei  is specified (as in this case, where it is assumed normal), one can estimate the parameters  b0 ,  b1 and s2  by the maximum likelihood (ML) method.  In essence, the ML method "chooses as estimates those values of the parameters that are most consistent with the sample data" (ALSM4e p. 30).

1.  ML Estimation of the Mean m

Assume Y normally distributed and variance known (s = 10); estimate mean m from sample with n = 3 (Y1 = 250, Y2 = 265, Y3 = 259).
Given an estimate of m, the likelihood L of the sample (Y1, Y2, Y3) is the product of the probability densities of the Yi given the value of the estimated mean.
The normal probability density function is f(Y) = (1/(SQRT(2p)s)) exp(-(1/2)((Y- m)/s)2)  (ALSM4e Appendix A, Theorem A.34).
Example:
If m = 230, then f(Y1)  = 0.053991, f(Y2)  = 0.000873, f(Y3) = 0.005953 so that
L (m = 230) = (0.053991)(0.000873)(0.005953) = (.279)10-6


Similarly, if m = 259, then

L (m = 259) = (0.333225)(0.398942)(0.266085) = 0.035373
Thus, the likelihood that m = 259 is greater than the likelihood of m = 230.
(NOTE:  Figures for the densities in NKNW p. 31 are incorrect; they are all shifted 1 decimal place to the right.)
Graphically the situation is as in the next exhibit: One could calculate the likelihood of the sample over a range of closely-spaced values of  m and graph the resulting likelihood function of  m.  as in the following exhibit: The value of  m corresponding to the maximum of the likelihood function (here m = 258) is the ML estimate of  m.  In practice the value(s) of the parameter(s) that maximize the likelihood function are found by iterative numerical optimization methods.

2.  ML Estimation of the Normal Regression Model

The principle for ML estimation of regression model is the same as for m. The likelihood function is as shown in NKNW Equation 1.26 p. 34.
The ML estimates of   are the values that maximize this likelihood function.
For teh simple regression model they are:
 
Parameter
ML Estimator
Remark
b0
^b0 = b0
same as OLS
 b1
^b1 = b1
same as OLS
s2
^s2  = SSE/n
<> OLS (MSE = SSE/(n-2))

NOTE: maximum likelihood derivations often use the logarithm (base e) of L rather than L itself.  See NKNW Equation 1.29 p. 35.

7.  Statistical Inference in Practice

1.  SYSTAT Commands for Simple Regression

The following printout shows how to obtain the simple regression of % clerks on seasonality, plot the corresponding scatterplot with the estimated regression line and the 95% Working-Hotelling confidence band, and how to get s{^Yh} for Xh = 35 (a value of seasonality that does not correspond to any case in the data set) by adding a dummy case with SEASON = 35 and missing value for CLERKS.

>USE "Z:\mydocs\S208\craft.syd"
SYSTAT Rectangular file Z:\mydocs\S208\craft.syd,
created Thu Nov 07, 2002 at 08:24:57, contains variables:
 TYPE$        SIZE         SEASON       CLERKS

>regress
>rem can also use command MGLH instead of REGRESS
>model clerks=constant+season
>estimate

Dep Var: CLERKS   N: 9   Multiple R: 0.852   Squared multiple R: 0.726

Adjusted squared multiple R: 0.687   Standard error of estimate: 2.103

Effect         Coefficient    Std Error     Std Coef Tolerance     t   P(2 Tail)

CONSTANT            14.631        1.700        0.000      .       8.607    0.000
SEASON              -0.169        0.039       -0.852     1.000   -4.311    0.004

Analysis of Variance

Source             Sum-of-Squares   df  Mean-Square     F-ratio       P
Regression                82.199     1       82.199      18.583       0.004
Residual                  30.963     7        4.423
-------------------------------------------------------------------------------

Durbin-Watson D Statistic          1.995
First Order Autocorrelation       -0.107

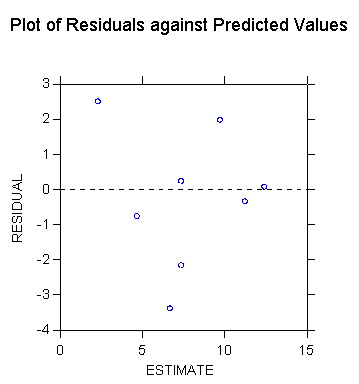
>rem show a scatterplot with the regression line
>rem and the Working-Hotelling 95% confidence band
>plot clerks*season/stick=out smooth=linear short confi=0.95

>rem now add a case with Xh=35, missing Y, using menus
>rem redo the estimation and save residuals to get SEPRED
>model clerks=constant+season
>save clerkres
>estimate

1 case(s) deleted due to missing data.

<...repeat output deleted...>

Residuals have been saved.

>use clerkres
SYSTAT Rectangular file Z:\mydocs\s208\clerkres.SYD,
created Fri Nov 15, 2002 at 10:20:07, contains variables:
 ESTIMATE     RESIDUAL     LEVERAGE     COOK         STUDENT      SEPRED

>list estimate residual sepred
  Case number     ESTIMATE     RESIDUAL       SEPRED
        1            2.311        2.489        1.485
        2            7.374        0.226        0.714
        3            9.737        1.963        0.814
        4            6.699       -3.399        0.759
        5            7.374       -2.174        0.714
        6            9.737        1.963        0.814
        7           11.256       -0.356        1.038
        8           12.437        0.063        1.254
        9            4.674       -0.774        1.035
       10            8.724         .           0.723

>rem SEPRED = 0.723 for SEASON=35 is same as calculated by hand earlier

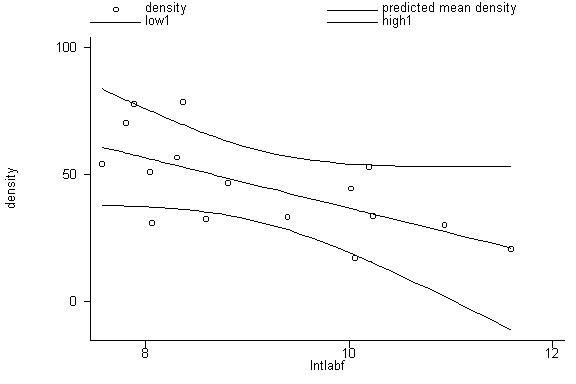
2.  STATA Commands

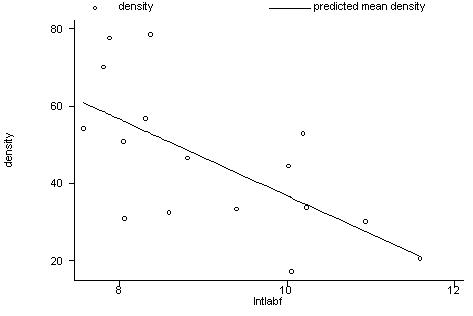
. reg density lntlabf

  Source |       SS       df       MS                  Number of obs =      16
---------+------------------------------               F(  1,    14) =   10.28
   Model |  2260.31012     1  2260.31012               Prob > F      =  0.0063
Residual |  3078.52104    14   219.89436               R-squared     =  0.4234
---------+------------------------------               Adj R-squared =  0.3822
   Total |  5338.83116    15  355.922077               Root MSE      =  14.829

------------------------------------------------------------------------------
 density |      Coef.   Std. Err.       t     P>|t|       [95% Conf. Interval]
---------+--------------------------------------------------------------------
 lntlabf |  -9.889076   3.084457     -3.206   0.006      -16.50458   -3.273573
   _cons |   135.7141    28.3748      4.783   0.000       74.85625     196.572
------------------------------------------------------------------------------

. predict yhat
[option xb assumed; fitted values]
. label variable yhat "predicted mean density"
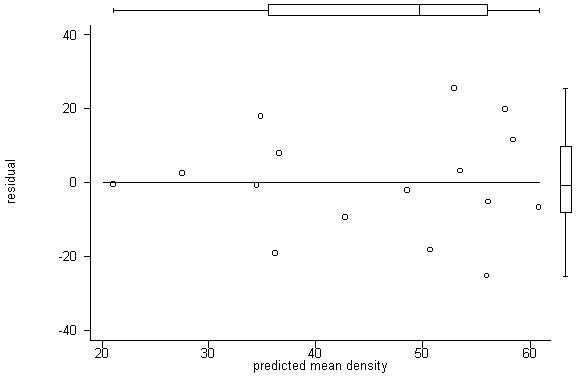
. predict e, resid
. label variable e "residual"
. generate yhat0=_b[_cons] + _b[lntlabf]*lntlabf
. generate e0=density-yhat0
. predict new, stdp
. graph density yhat lntlabf, connect(.s) symbol (Oi) ylabel xlabel
 

. graph e yhat, twoway box yline(0) ylabel xlabel


 

. display invttail(14,.025)
2.1447867
[If you’d rather use the F-value here, use the command invFtail (dfn,dfd, p)]
. generate low1=yhat-2.1448*new
. generate high1=yhat+2.1448*new
. graph density yhat low1 high1 lntlabf, connect(.sss) symbol(Oiii) ylabel xlabel


 

10.  Historical Note

1.  The Normal Distribution

The discoveries of the normal probability distribution and of the central limit theorem are associated with mathematicians Pierre Simon Laplace and Carl Friedrich Gauss. Q - What languages are Laplace and Gauss using in these excerpts?  Why?

2.  The Student t Distribution

The Student t distribution was discovered by William Gosset.

Q - Do you know the origin of the name "Student"?


Last modified Jan 2006