SOCI709 (formerly 209) - Module 3 - Diagnostics & Remedies in Simple Regression

1.  Residual Analysis & the Healthy Regression

1.  Residual Plot of the Healthy Regression

Residual analysis is a set of diagnostic methods for investigating the appropriateness of a regression model based on the residuals
ei = Yi - ^Yi
where ^Yi is the fitted value (aka predictor, aka estimate)
^Yi = b0 + b1Xi
The basic idea is that, if the regression model is appropriate, the residuals ei should "reflect the properties ascribed to the model error terms ei", such as independence, constant variance for different levels of X and normal distribution.  The workhorse of residual analysis is the residual plot, or plot of the residuals ei against the fitted values
^Yi = b0 + b1Xi.
In a healthy regression the residuals should appear as arranged randomly in a horizontal band around the Y = 0 line, like so

In reality, computer programs typically adapt the range of the data to occupy the entire frame of the plot, so that the residuals appear as a random cloud of points spread out over the entire vertical range of the plot.  The next exhibit shows a typical computer-generated residual plot

2.  Potential Problems With the Simple Regression Model

Problems with the regression are departures from ( or violations of) the assumptions of the regression model.  They are:
  1. Regression function is not linear
  2. Error terms do not have constant variance
  3. Error terms are not independent
  4. Model fits all but one or a few outlier observations
  5. Error terms are not normally distributed
  6. One or several important predictor variables have been omitted from model
These problems also affect multiple regression models.  Most of the diagnostic tools used for simple linear regression are also used with multiple regression.
This module examines these potential problems in conjunction with diagnostic tools which can be informal (such as graphs) or formal (such as tests), and remedies.

3.  Using Informal (Graphic) Versus Formal Diagnostic Tests

Features of informal graphic diagnostics are Features of formal tests are Researchers can use available informal and formal diagnostics to develop their own strategy to diagnose problems with their models.

2.  Regression Function is Not Linear

1.  Scatterplot or Residual Plot With LOWESS Robust Nonparametric Regression Curve (Diagnostic, Informal)

Nonlinearity in the regression function may appear in the scatter plot of Y versus X, or in the residual plot.  The residual plot often magnifies nonlinearity (compared to the scatter plot) and makes it more noticeable.  A nonlinear trend may be revealed by using a nonparametric regression technique such as LOWESS.  The LOWESS algorithm estimates a curve that represents the main trend in the data, without assuming a specific mathematical relationship between Y and X.  (This is why it is called nonparametric.)  The next two exhibits show (1) a scatterplot of female life expectancy against doctors per million for 137 countries in 1975, and (2) a plot of the residuals of the regression of female life expectancy on doctors per million.  Note how the nonlinearity is magnified by the residual plot, as compared to the plot of Y against X. LOWESS (aka LOESS) was invented by William S. Cleveland (1994:168-180, 1993:94-101).

2.  Linearity or Lack of Fit Test (Diagnostic, Formal, Limited Applicability)

There is a test of linearity of the regression function, called the lack of fit test.  This test requires repeat observations (called replications) at one or more levels of X, so it cannot be performed with all data sets. In essence it is a test of whether the means of Y for the groups of replicates are significantly different from the fitted value ^Y on the regression line, using a kind of F test.  The test is explained in ALSM5e pp. 119-127; ALSM4e pp. 115-124.

3.  Polynomial Regression (Remedy)

Some forms of non-linearity can be modeled by introducing higher powers of X in the regression equation.  Polynomial regression is a form of multiple regression and is discussed in Module 6 - Polynomial Regression & Interactions.

4.  Transforming Variables To Linearize the Relationship (Remedy)

1.  Error Variance Appears Constant
When the error variance appears to be constant, only X needs be transformed to linearize the relationship.  Some typical situations are shown in the next exhibit. The following exhibit shows an example of a non-linear regression function that can be straightened by transforming X.
2.  Error Variance Appears Not Constant
When the error variance does not appear constant it may be necessary to transform Y or both X and Y.  The next two exhibits show examples.
3.  Transformation to Simultaneously Linearize the Relationship and Normalize the Distribution of Errors
See Box-Cox transformation under 6.2 below.

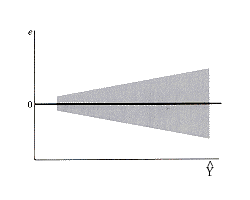
3.  Error Terms Do Not Have Constant Variance (Heteroskedasticity)

1.  Funnel-Shape in in Residual Plot (Diagnostic, Informal)

Terminology:
homoskedasticity:  s2 is constant over the entire range of X (as specified by OLS assumptions)
heteroskedasticity:  s2 is not constant over the entire range of X (departure from OLS assumptions)
The regression model assumes homoskedasticity.  Heteroskedasticity may be manifested by a funnel or megaphone pattern like the following prototype

A real example is Sometimes the funnel pattern is reversed, with greater error variance corresponding to smaller values of X. Q - Why is the variance in depression score lower for higher incomes and vice-versa?

However, when the residual is plotted against ^Y the megaphone pattern fans out to the right.  (Why?)

2.  Plot of Absolute Residual |e| or Squared Residual e2 by ^Y (Diagnostic, Informal)

A pattern of heteroskedasticity can be detected informally by plotting the absolute residual or the squared residual against ^Yi; adding the linear fit or a LOWESS curve helps seeing the trend in the data:

3.  Tests for Homoskedasticity (Constancy of s2 ) (Diagnostic, Formal)

There are many tests of heteroskedasticity.  Three formal tests of constancy of the error variance will be discussed in Module 12 - Heteroskedasticity & Weighted Least Squares: (The Breusch-Pagan aka Cook-Weisberg Test can be carried out in STATA with the command hettest following the regress command.  An example will be shown in the hands-on session.)

4.  Variable Transformation To Equalize the Variance of Y (Remedy)

See Section 6 below on Tukey's ladder of powers and the Box-Cox transformation.  Transformations of Y to make the distribution of residuals normal often have the effect of also equalizing the variance of Y over the entire range of X.

5.  Weighted Least Squares (Remedy)

In rare cases where a variable transformation that takes care of unequal error variance cannot be found, one can use weighted least squares.  In weighted least squares observations are weighted in inverse proportion to the variance of the corresponding error term, so that observations with high variance are downweighted relative to observations with low variance.  Weighted least squares is discussed in Module 12 - Heteroskedasticity & Weighted Least Squares.

4.  Error Terms Are Not Independent

1.  Residual e by Time or Other Sequence (Diagnostic, Informal)

In time series data where observations correspond to successive time points, errors can be autocorrelated or serially correlated.  Such a pattern can be seen in a plot of residuals against the time order of the observations, as in the following prototype

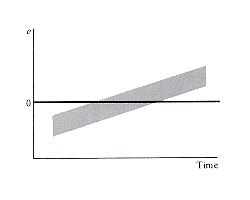
The following real example shows residuals for a regression of the divorce rate on female labor force participation (U.S. 1920-1996).  Note the characteristic "machine gun" tracking pattern.  The residual is plotted against the index of a case (corresponding to a year of observation). Q - What year is the peak divorce residual?

Remedial techniques for lack of independence are discussed in Module 14 - Autocorrelation in Time Series Data.

2.  Durbin-Watson Test of Independence (Diagnostic, Formal)

See Module 14 - Autocorrelation in Time Series Data.

5.  Model Fits All But One Or A Few Outlier Observations

1.  Outliers in Scatterplot or Residual Plot (Diagnostic, Informal)

Outliers may often (but not always) be spotted in a scatterplot or residual plot. Outlying observations may affect the estimate of the regression parameters, as shown in the following exhibit. Outlying observations may sometimes be identified in a box plot or stem-and-leaf display of the residuals (see below).

2.  Tests for Outlier and Influential Cases (Diagnostic, Formal)

An extensive discussion of outliers and influential cases is provided in Module 10 - Outlying & Influential Observations.

6.  Error Terms Are Not Normally Distributed

Non-normality of errors corresponds to a range of issues with different degrees of severity.  Kurtosis (fat tails) and skewness are more serious than more minor departures from the normal.  These features of the distribution blend in with the problem of outlying observations.

1.  Box Plot, Stem-and-Leaf, and Other Displays of the Distribution of e (Diagnostic, Informal)

Lack of normality (as well as some types of outlying observations) may be diagnosed by looking at the distribution of the residuals using devices such as a histogram, stem and leaf display, box plot, kernel density estimator, etc.   In the following examples see how the histogram of the distribution appears normal but fat tails/outlying observations are revealed in other displays.

2.  Normal Probability Plot of e (Diagnostic, Informal)

The normal probability plot is used to examine whether the residuals are normally distributed.  It is a plot of the residuals against their expected values assuming normality.  The expected values of the residuals are obtained by first sorting them in increasing order of magnitude.  Then
EXPECTEDk = z((k - 0.5)/n) for k=1,...,n
where k is the rank of the residual such that k = 1 for the smallest value of e and k = n for the largest, z((k - 0.5)/n) is the 100((k - 0.5)/n) percentile of the standard normal distribution N(0,1).
When the residuals are normally distributed, the plot is approximately a straight line. Notes: The shape of normal probability plot reveals aspects of the distribution of e. The following exhibits show a full example of calculation of the probability plot based on the Yule data set.

3.  Correlation Test for Normality (Diagnostic, Formal)

The correlation test for normality is based on the normal probability plot.  It is the correlation between the residuals ei and their expected values under normality.  The higher the correlation, the straighter the normal probability plot, and the more likely that the residuals are normally distributed.  The value of the correlation coefficient can be tested, given the sample size and the a level chosen, by comparing it with the critical value in Table B.6 in ALSM5e/4e.  A coefficient larger than the critical value supports the conclusion that the error terms are normally distributed (ALSM5e pp. 115-116; ALSM4e p. 111).
Example: For the Yule data the correlation between residual and value expected under the normality assumption is .981 with n=32.  Table B.6 in ALSM5e/4e gives the critical values for n = 30 of .964 with a=.05.  Since r=.981 > .964 one concludes that the residuals are normally distributed.

4.  Data Transformations Affecting the Distribution of a Variable (Remedy)

This section relies extensively on Wilkinson, Blank, and Gruber (1996, Chapter 22 pp. 695-713).
1.  Standardizing a Variable - Does Not Affect Shape of Distribution
Common variable standardizations are the z-score and range standardization.  These transformations do not affect the shape of the distribution of the variable (contrary to some popular beliefs).

The standardized value Z of Y is obtained by the formula

Z = (Y - Y.) / sY
where Y. and sY denote the sample mean and standard deviation of Y, respectively.
The range-standardized value W of Y is obtained by the formula
W = (Y - YMIN) / (YMAX - YMIN)
where YMAX and YMIN denote the maximum and minimum values of Y, respectively.
2.  Transforming a Variable to Look Normally Distributed
Transformations of Y can be used to remedy non-normality of the error term.
a.  Radical normalization with the rankit transformation
The rankit transformation transforms any distribution into a normal one.  It is the same as grading on the curve.  It is the same as finding the expected value of the residual in preparing a normal probability plot.
b.  Tukey's ladder of powers
Tukey (1977) has proposed a ladder of powers spanning a range of transformations to normalize the distribution of a variable in a data set.
c.  Automatic choice of ladder of powers transformation with the Box-Cox procedure
The family of power transformations in Tukey's ladder is of the form
Y' = Yl
where l is the power parameter.  Some of the principal steps of the ladder are
 
Lambda (l)
 Transformation Name
2
 Y' = X2 square
1
 Y' = X identity
.5
 Y' = (X)1/2 square root
0
 Y' = log(X) logarithm (any base)
-.5
 Y' = 1/(X)1/2 inverse square root
-1
 Y' = 1/Y inverse

but l can take any value in between.
In the simplest version the Box-Cox procedure estimates the parameter l by maximum likelihood so as to maximize the fit of the transformed data Y' to a normal distribution.  There is only one variable involved.

Example: Find the transformation of V181 (female life expectancy) that best normalizes the distribution.  STATA estimates lambda as
 
lambda Std. Error z (same as t*) P{|Z|>z} CI Low CI Up Sigma
 .1362285  .0660046  2.06 .039  .0068619 .265595 3.136496

The program does chi-square tests of 3 hypotheses on the value of lambda:
 
H0: l =
 Chi-square P-value
-1
 300.88 .000
0
 4.35 .037
1
 140.35 .000
So estimated l (.1362285) is close to 0 (logarithm transformation), but H0: l = 0 is rejected at the .05 level (although not at the .01 level).

d.  Box-Cox procedure to optimize the linear relationship between X and Y
The Box-Cox procedure can also be used to transform Y and X in such a way as to maximize their relationship.  The procedure can estimate an exponent q (theta) of X as well as the exponent l (lambda) of Y.  The complete model is thus
Yil = b0 + b1Xiq + ei
The estimates l, b0 ,  b1 and s2  can be found by maximizing the likelihood function shown in ALSM5e p. 135, Equation 3.36; ALSM4e p. 135, Equation 3.35.  There are now two variables involved, Y and X.  (The model generalizes to multiple regression, with some limitations.)
In the following example v195 is Female Life Expectancy 1975 and v181 is Doctors per Million 181.  The estimates are
 
Coefficient Coefficient Std. Error  z (same as t*) P{|Z|>z} 95% CI Low 95% CI Up
lambda .1772316 .0705726 2.51 0.012 .0389119 .3155514
theta 1.422054 .3605058 3.94 0.000 .7154761 2.128633
V181 16.74134 Sigma =  31.67667

Note that the exponent theta for X is 1.422, but the 95% CI includes 1.0 so one cannot reject the hypothesis that the optimal theta is 1.0 (optimal transformation is no transformation).
On the Box-Cox procedure see ALSM5e pp. 134-137.

d.  Arcsine transformation for proportions and percents
Proportions and percentages often produce a truncated and skewed distribution when the mean is not near .5.  The arcsine transformation corrects these problems.  Use
let ynew = 2*asn(sqr(P))
where P is a proportion.  (Transform percentages to proportions by dividing by 100 before applying transformation.)
e.  Fisher's z transformation for correlation coefficients
Correlation coefficients often produce a truncated and skewed distribution when the mean is not near 0.  Fisher's z transformation (aka hyperbolic tangent) normalizes such distributions.  Use
let ynew = ath(R)
where R is a correlation between -1 and +1.

7.  One or Several Important Predictor Variables Have Been Omitted From Model

Plot of Residual e by Omitted Predictor Variable Z

Z is a potential predictor variable that is not included in the equation.

8.  Simple Regression Diagnostics & Remedies in Practice

1.  SYSTAT Examples

>USE "Z:\mydocs\ys209\survey2b.syd"
[...deleted output...]
>regress
>model total=constant+income
>save resid/data
>estimate

Dep Var: TOTAL   N: 256   Multiple R: 0.210   Squared multiple R: 0.044

Adjusted squared multiple R: 0.040   Standard error of estimate: 8.728

Effect         Coefficient    Std Error     Std Coef Tolerance     t   P(2 Tail)
CONSTANT            11.811        0.948        0.000      .      12.461    0.000
INCOME              -0.120        0.035       -0.210     1.000   -3.425    0.001

Analysis of Variance
Source             Sum-of-Squares   df  Mean-Square     F-ratio       P
Regression               893.479     1      893.479      11.729       0.001
Residual               19348.271   254       76.174

*** WARNING ***
Case          256 is an outlier        (Studentized Residual =        4.598)

Durbin-Watson D Statistic          0.659
First Order Autocorrelation        0.631

Residuals and data have been saved.


 

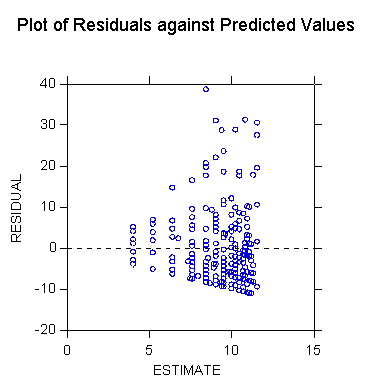
>use resid

SYSTAT Rectangular file Z:\mydocs\s208\resid.SYD,
created Mon Jan 20, 2003 at 10:04:34, contains variables:

 ESTIMATE     RESIDUAL     LEVERAGE     COOK         STUDENT      SEPRED
 ID           SEX          AGE          MARITAL      EDUCATN      EMPLOY

[...deletd output...]

>let absres = abs(residual)
>plot absres*estimate/stick=out smooth=lowess
 

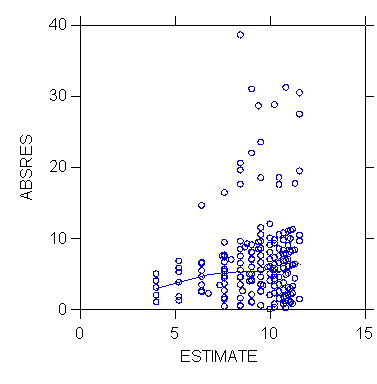
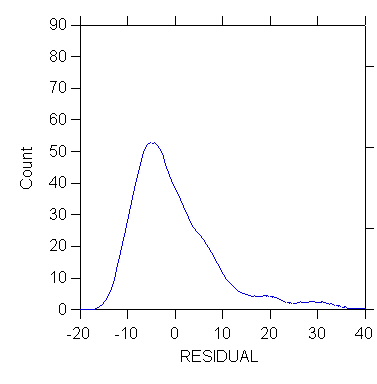
>den residual/stick=out kernel

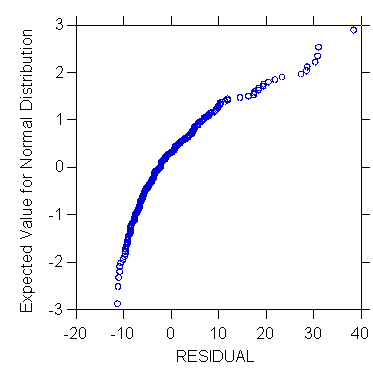
>pplot residual/stick=out

>rem calculate expected residuals under normality explicitly
>rem to do correlation test
>sort residual

  256 cases and 56 variables processed.

>let resrank = case
>list residual resrank/n=10

  Case number     RESIDUAL      RESRANK
        1          -11.212        1.000
        2          -11.092        2.000
        3          -10.973        3.000
        4          -10.733        4.000
        5          -10.733        5.000
        6          -10.494        6.000
        7          -10.015        7.000
        8           -9.733        8.000
        9           -9.571        9.000
       10           -9.536       10.000

>let expres = zif((resrank - 0.5)/256)
>rem next plot should be same as pplot command
>plot expres*residual/stick=out


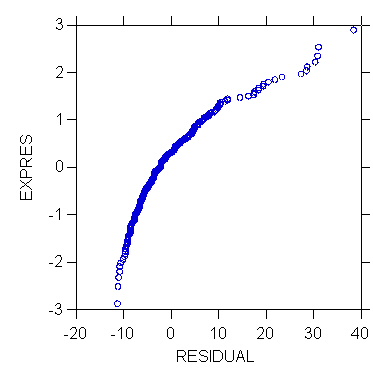
>corr
>pearson expres*residual

Pearson correlation matrix

                  RESIDUAL

 EXPRES              0.926

Number of observations: 256

>rem test for normality using correlation test and
>rem ALSM5e Table B.6
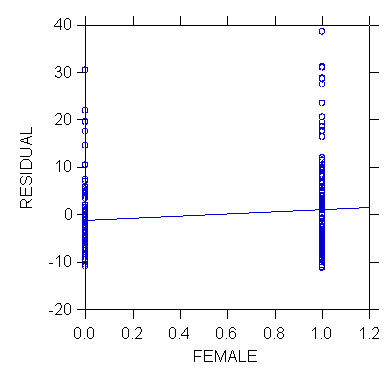
>plot residual*female/stick=out smooth=linear


>den income/stick=out kernel

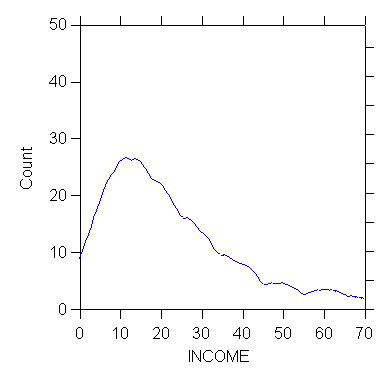
>den income/stick=out kernel
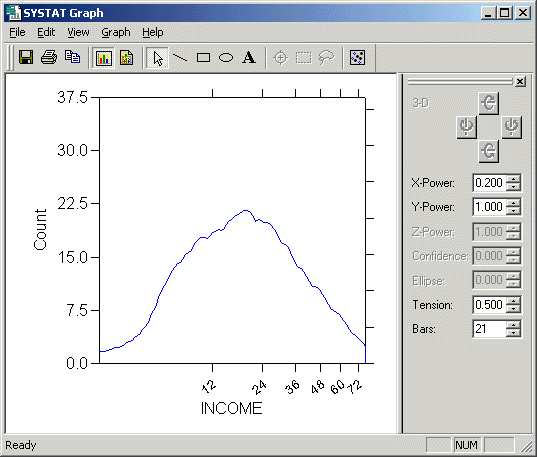
>rem the kernel density of income is "normalized" by setting the power
>rem exponent interactively after double-clicking on the graph, as shown
>rem in following picture


 

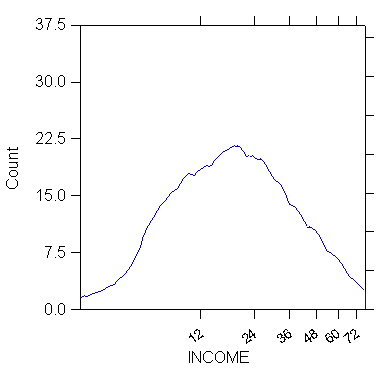
>rem this yields the kernel density with power exponent = 0.2
 

>USE "Z:\mydocs\ys209\world209.syd"

[...deleted output...]

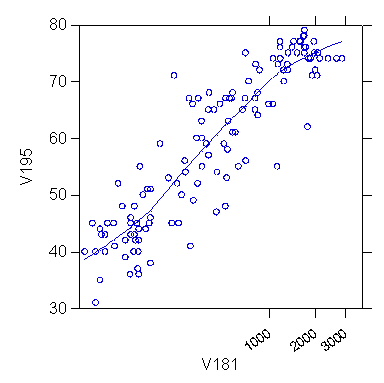
>plot v195*v181/stick=out smooth=lowess
 


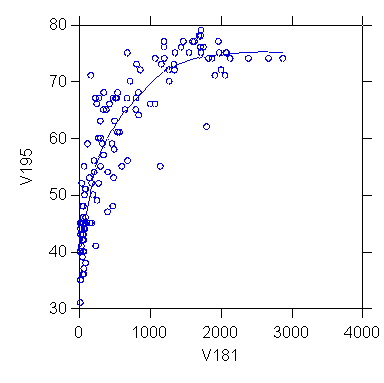
>rem scatterplot with LOWESS curve shows strong non-linear
>rem pattern; relationship "straightend" by setting power
>rem exponent of V181 to 0.2 interactively after double-
>rem clicking on graph


 

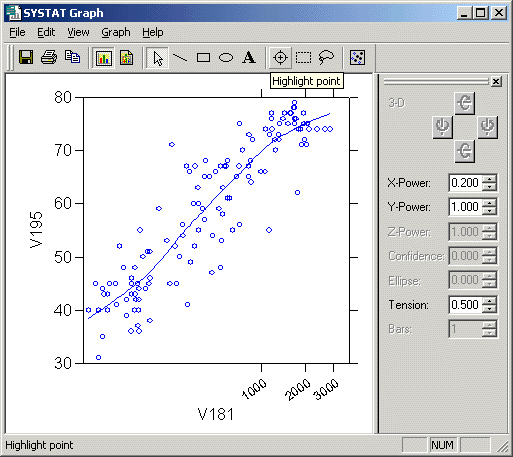
>plot v195*v181/stick=out smooth=lowess


 

2.  STATA Examples

(By Catherine Harnois and Cheol-Sung Lee, TAs in Spring 2003.)
 
We highly recommend the UCLA STATA module for diagnostics
. use "C:\Stata\auto.dta", clear
*1978 Automobile Data

. boxcox mpg, nolog level(95)

Transform:  (mpg^L-1)/L

                 L       [95% Conf. Interval]     Log Likelihood
            ----------------------------------------------------
              -0.3584      -1.1296     0.4078          -123.2664

     Test:  L == -1      chi2(1) =     2.68    Pr>chi2 =  0.1018
            L ==  0      chi2(1) =     0.82    Pr>chi2 =  0.3649
            L ==  1      chi2(1) =    12.25    Pr>chi2 =  0.0005

*nolog level(95) tells Stata not to display the iterations log but to include
 a 95% confidnence interval. The interval rejects the hypothesis that the best
 transformation is no transformation.
*next create a new variable newmpg based on the optimal exponent found by boxcox procedure
. gen newmpg = (mpg^(-0.3584) - 1)/(-0.3584)
*next compare distributions of mpg and newmpg
. graph mpg, bin(10) ylabel xlabel norm t1(raw data)

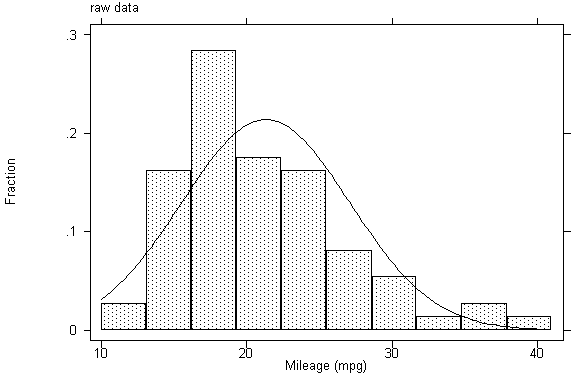
. graph newmpg, bin(10) ylabel xlabel norm t1(transformed data)
 

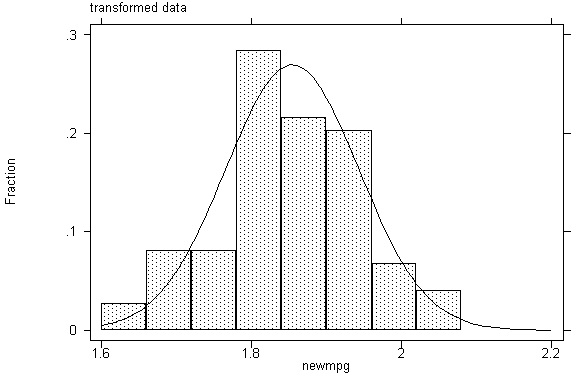
. kdensity mpg, normal border
 

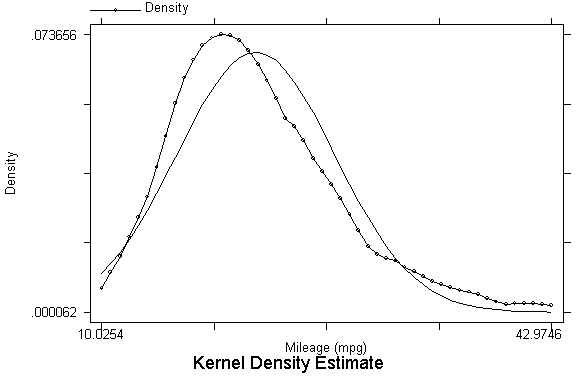
. kdensity newmpg, normal border

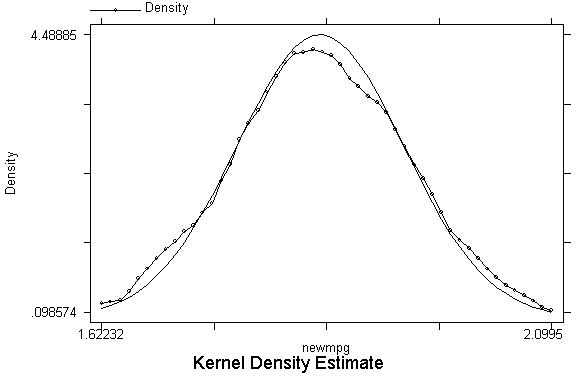
. ksm mpg weight, lowess xlab ylab border
 


 

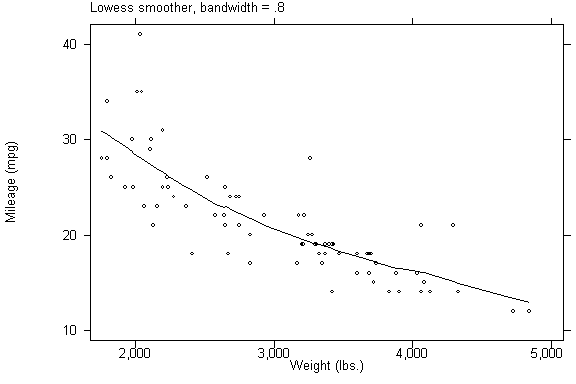
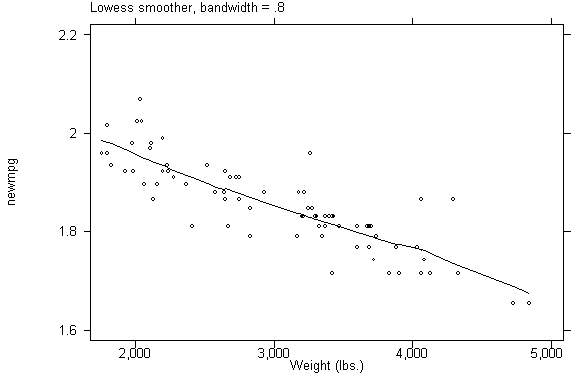
. ksm newmpg weight, lowess xlab ylab border

. stem mpg

Stem-and-leaf plot for mpg (Mileage (mpg))

  1t | 22
  1f | 44444455
  1s | 66667777
  1. | 88888888899999999
  2* | 00011111
  2t | 22222333
  2f | 444455555
  2s | 666
  2. | 8889
  3* | 001
  3t |
  3f | 455
  3s |
  3. |
  4* | 1

. ladder mpg

Transformation         formula             Chi-sq(2)     P(Chi-sq)
------------------------------------------------------------------
cube                   mpg^3                  43.59        0.000
square                 mpg^2                  27.03        0.000
raw                    mpg                    10.95        0.004
square-root            sqrt(mpg)               4.94        0.084
log                    log(mpg)                0.87        0.647
reciprocal root        1/sqrt(mpg)             0.20        0.905
reciprocal             1/mpg                   2.36        0.307
reciprocal square      1/(mpg^2)              11.99        0.002
reciprocal cube        1/(mpg^3)              24.30        0.000

In this formula, m=mu and s=the standard deviation and I is the observation number.

. pnorm mpg
 


 

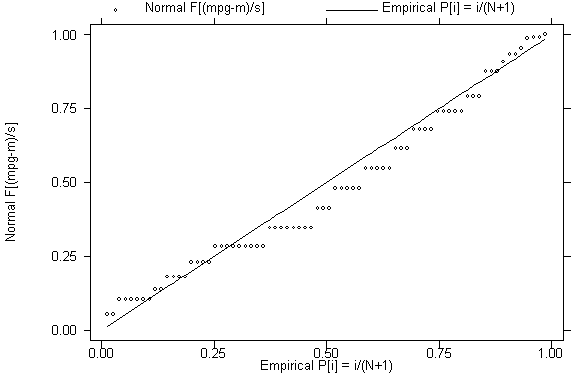
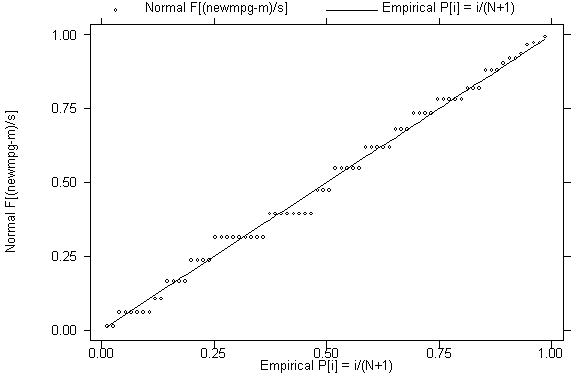
. pnorm newmpg


 

. regress mpg weight

  Source |       SS       df       MS                  Number of obs =      74
---------+------------------------------               F(  1,    72) =  134.62
   Model |   1591.9902     1   1591.9902               Prob > F      =  0.0000
Residual |  851.469256    72  11.8259619               R-squared     =  0.6515
---------+------------------------------               Adj R-squared =  0.6467
   Total |  2443.45946    73  33.4720474               Root MSE      =  3.4389

------------------------------------------------------------------------------
     mpg |      Coef.   Std. Err.       t     P>|t|       [95% Conf. Interval]
---------+--------------------------------------------------------------------
  weight |  -.0060087   .0005179    -11.603   0.000      -.0070411   -.0049763
   _cons |   39.44028   1.614003     24.436   0.000       36.22283    42.65774
------------------------------------------------------------------------------

. fpredict yhat

. fpredict e,resid
. graph e yhat
. rvfplot, oneway twoway box yline(0) ylabel xlabel

 


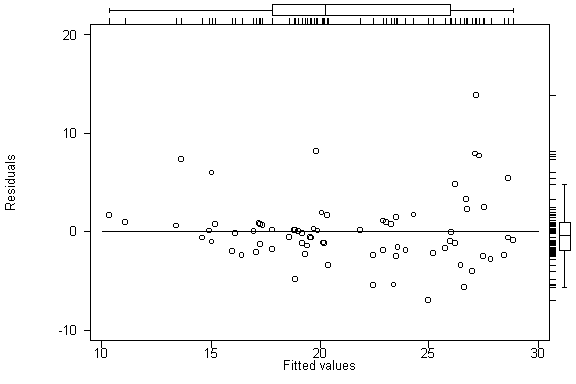
. hettest

Cook-Weisberg test for heteroscedasticity using fitted values of mpg
     Ho: Constant variance
         chi2(1)      =     11.05
         Prob > chi2  =      0.0009

. ovtest

Ramsey RESET test using powers of the fitted values of mpg
       Ho:  model has no omitted variables
                  F(3, 69) =      1.77
                  Prob > F =      0.1616
 

Appendix - Mathematical Functions

Mathematical and Satistical Functions Available in SYSTAT
Mathematical and Satistical Functions Available in STATA
Please consult STATA Manual


Last modified 30 Jan 2006